Treatment Thresholds & Value of Information

Learning Objectives and Outline

Learning Objectives

• Define treatment thresholds within a decision tree & examine different ways of interpretation

• Understand and calculate the value of information from a perfect vs. imperfect test

Outline

• Treatment thresholds

• Testing & Value of Information

Treatment thresholds

Treatment thresholds

• Let’s start with the PULMONARY EMBOLISM example that we’ve looked at before & in our text

• Pulmonary embolism (PE) during pregnancy is a life-threatening event. Treatment with anti-coagulation is effective in preventing further PE and hence in reducing the fatality probability.

• The choices here are either to ANTICOAGULATE OR TO NOT ANTICOAGULATE & our main objective is to optimize survival

• When we calculate out the probabilities, the overall expected survival chances with ANTICOAGULATION is 99%, compared to 95% WITHOUT ANTICOAGULATION

• Therefore, we would, on average, choose to ANTICOAGULATE in this case because it has higher overall survival

• BUT to be confident about our decision, we need to explore HOW our assumptions will affect the decision in sensitivity analyses

***We will cover more on SA’s later in the semester as it relates to cost-effectiveness analysis

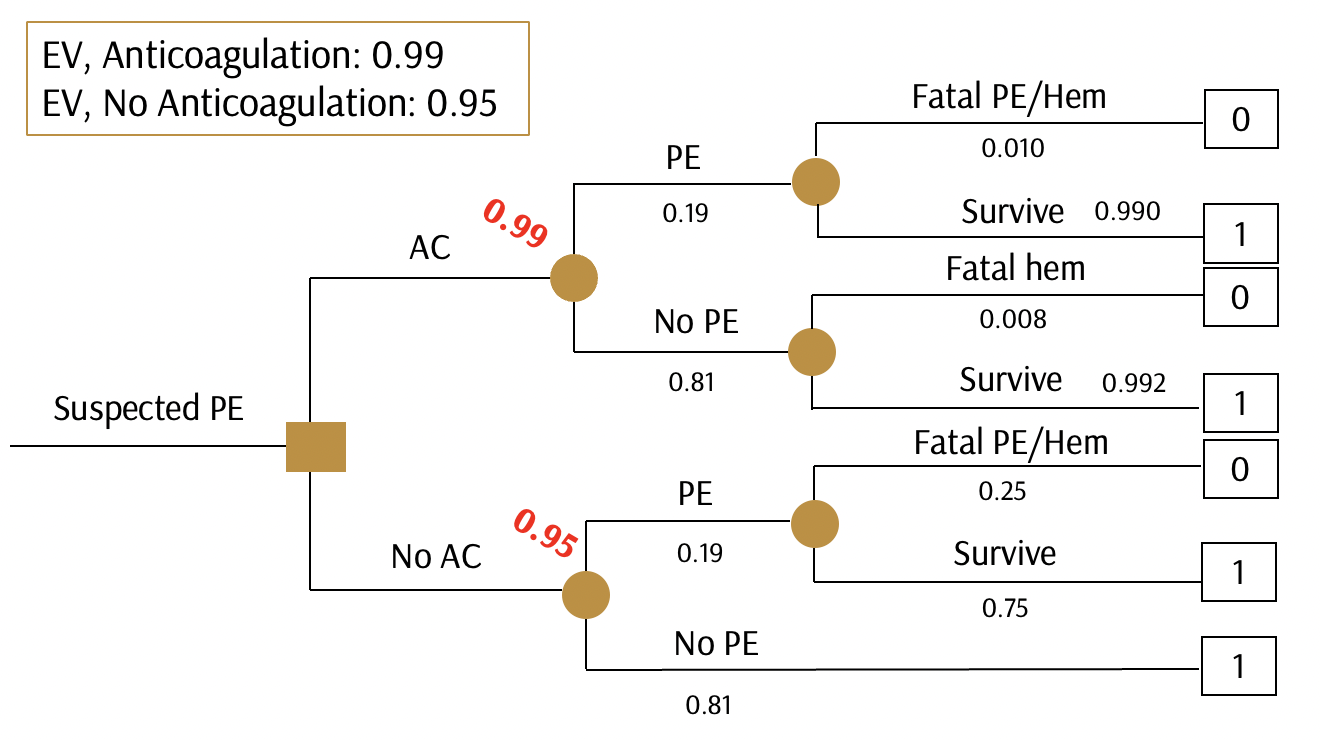
Treatment thresholds

What if the probability of recurrent PE were higher or lower than initially estimated?

• Do we anticoagulate or not?
• At what point do we switch between “yes” versus “no”?

• I know we touched on this briefly in the last couple of lectures in various forms, but the key question that we always need to ask in any decision problem is AT WHAT POINT DO WE SWITCH BETWEEN OPTIONS?

• In this case, what IF the probability of recurrent PE were higher or lower than initially estimated? would we still choose to anticoagulate? & at what point would we switch?

• (And from a cost-effectiveness perspective, at more of a higher population level - what variations will ultimately change our decision) – In this case, to anticoagulate versus not.

• Parameters will always have confidence intervals around them & will also be uncertain depending on our assumptions in our model & the information that we have.

• However, the more information we have on a certain disease/parameter, the more confidence we will have in our decisions.

Treatment thresholds

• From more of a clinical standpoint –

• Our THRESHOLD TO TREAT a patient is the point at which the expected value of treatment & no treatment are exactly EQUAL

  • Another way to look at this (which we’ll go over in the upcoming slides) is the RATIO of NET HARM of treating patients without the disease & BENEFIT gained by treating patients with the disease.

• And if we incorporate DIAGNOSTIC TESTING as part of our decision-making, we can determine how a patient’s risk might change based on the result of a particular test

  • For example, if the test has no chance of moving the patient’s risk above the treatment threshold, then the test should probably not be ordered. Because as we know, tests can also come with their own risks & costs.

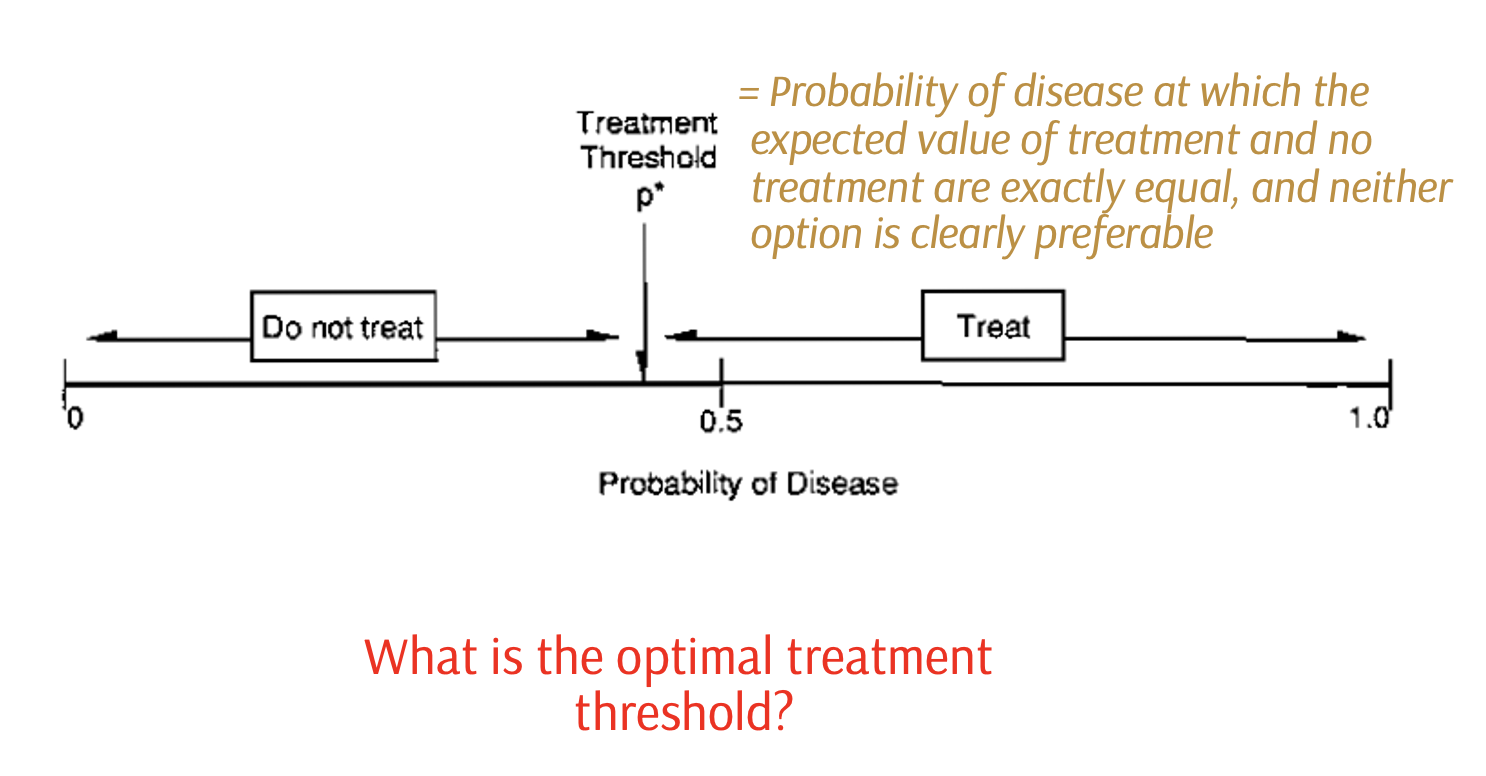
Treatment thresholds

Perform a sensitivity analysis to find a treatment threshold

(More on sensitivity analyses later in the workshop)

• We would need to perform a sensitivity analysis to find the treatment threshold

  • Similar to the “beach” example in the second class

Treatment thresholds

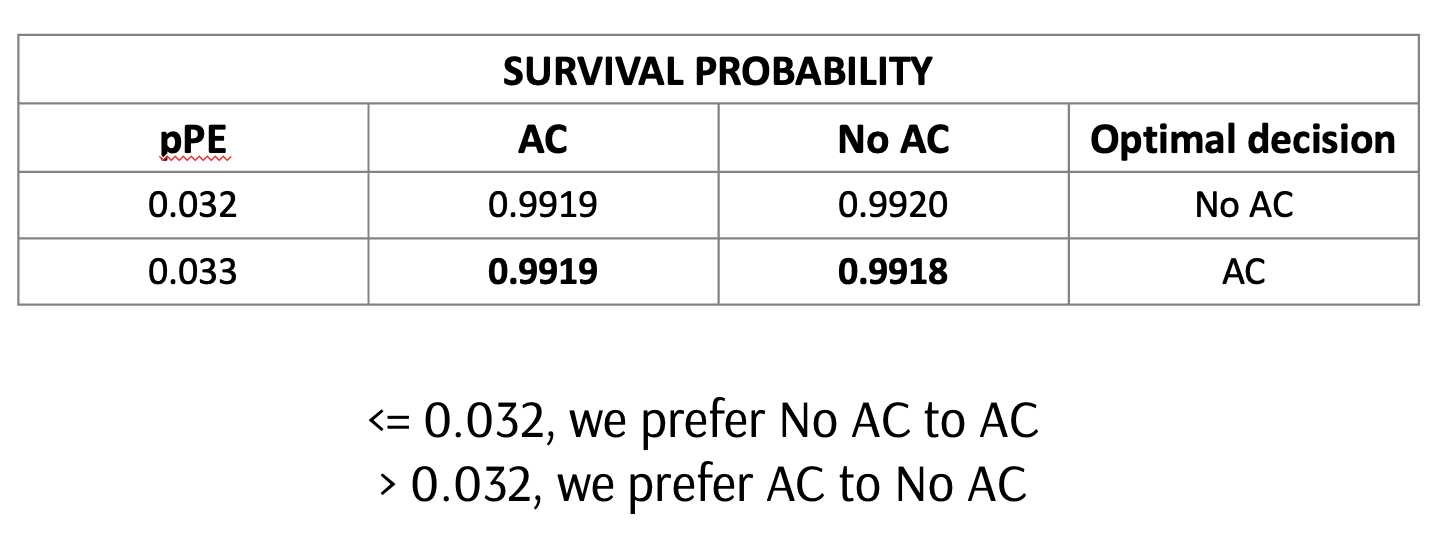
Expected value (AC) = 0.990 * pPE + 0.992 * (1-pPE)

Expected value (No AC) = 0.750 * pPE + 1.0 * (1-pPE)

NOW, SET EQUAL TO EACH OTHER, to solve for unknown threshold probability

• To go back to our PE example,

• A key parameter in our model is the probability of pulmonary embolism when we undergo anticoagulant treatment versus not.

• If we set the EXPECTED VALUE OF AC VERSUS NO AC equal to each other, like we’ve done in previous examples, we can solve for the unknown threshold probability

  • which is the point where the expected value of treatment and withholding treatment are exactly equal for this specific decision problem.

Treatment thresholds

0.990 * pPE + 0.992 * (1-pPE) = 0.750 * pPE + 1.0 * (1-pPE)

0.240 * pPE = 0.008 * (1-pPE)

0.240 * pPE + 0.008 *pPE = 0.008

pPE = 0.008 / (0.240 + 0.008)

= .032

Treatment thresholds

• So, what does this mean?

• If you put these probabilities for PE back into our model for each AC & no AC, then you’ll get these survival probabilities

• You can see the point in which our decision would change

• If our pPE is EQUAL TO or LESS THAN .032, then we would prefer no AC to AC

• But, as displayed in the second row, if our pPE is GREATER than .032, then we would prefer AC to No AC - bc higher overall survival

Treatment thresholds

• When we go back to thinking about testing & how that might impact our decision to treat…

• No tests should be done UNLESS the result of the test will change the treatment plan

  • So, on the top bar – the result of additional tests do not change our treatment plan
  • Whereas, looking at the bar below, additional tests could in fact change our treatment plan

• A key question we should be asking is - Is the risk of the test worth the benefit of getting it **** & this is something we can explore withing a decision analysis framework

Treatment thresholds

Performing a test to gain additional information is ONLY worthwhile IF:

1. At least one decision would change given some test results, and/or
   
   
2. The risk to the patient associated with the test is less than the expected benefit gained from undergoing the test

Treatment thresholds

Same as before, but here, the additional information you gain on the top bar, doesn’t change your decision NOT to treat

Treatment thresholds

You can look at test/treat thresholds the following way –

• DO NOT TREAT & DO NOT TEST – when even a positive test result will not persuade us to treat Ex. 95 year old, testing says you need a hip replacement. You’re likely not going to get the surgery due to the risks regardless of the positive result.
• TEST – if the test will help us make a treatment decision
• TREAT & DO NOT TEST – when even a negative test result will not dissuade us from treating Ex.

Treatment thresholds

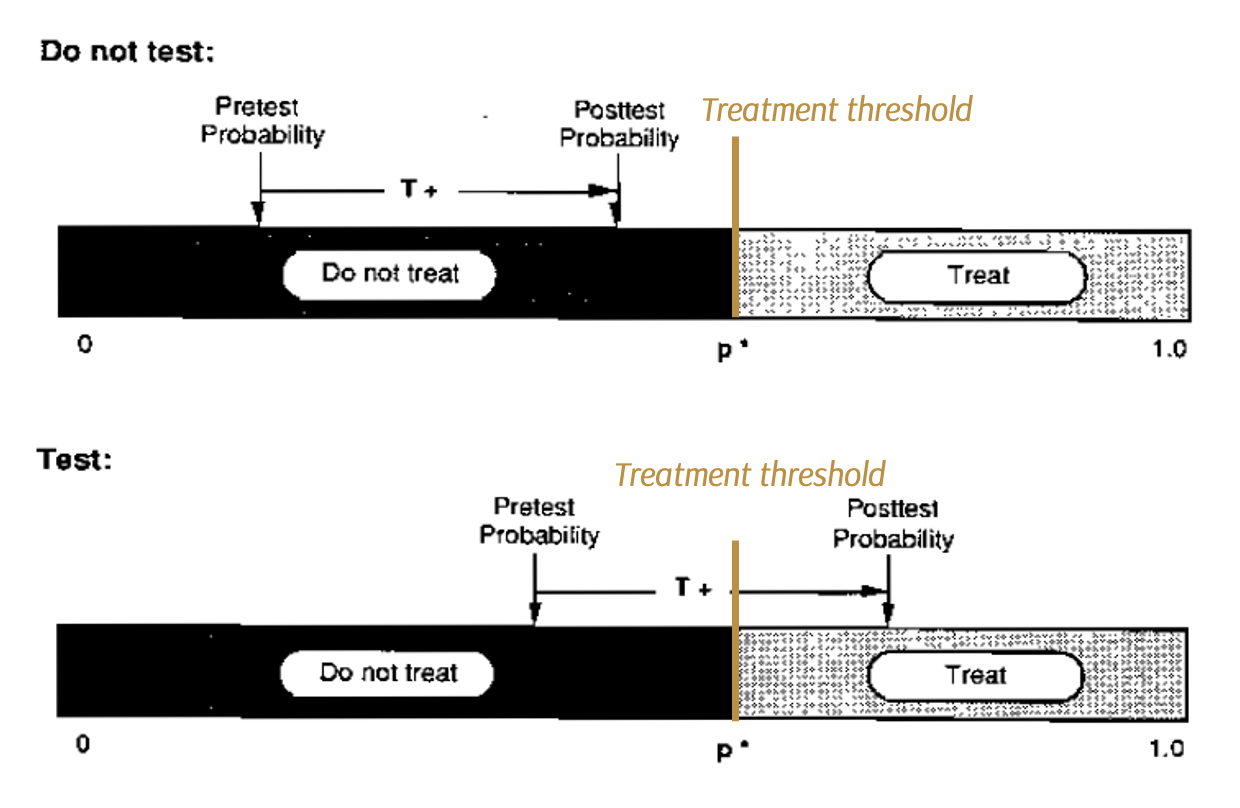
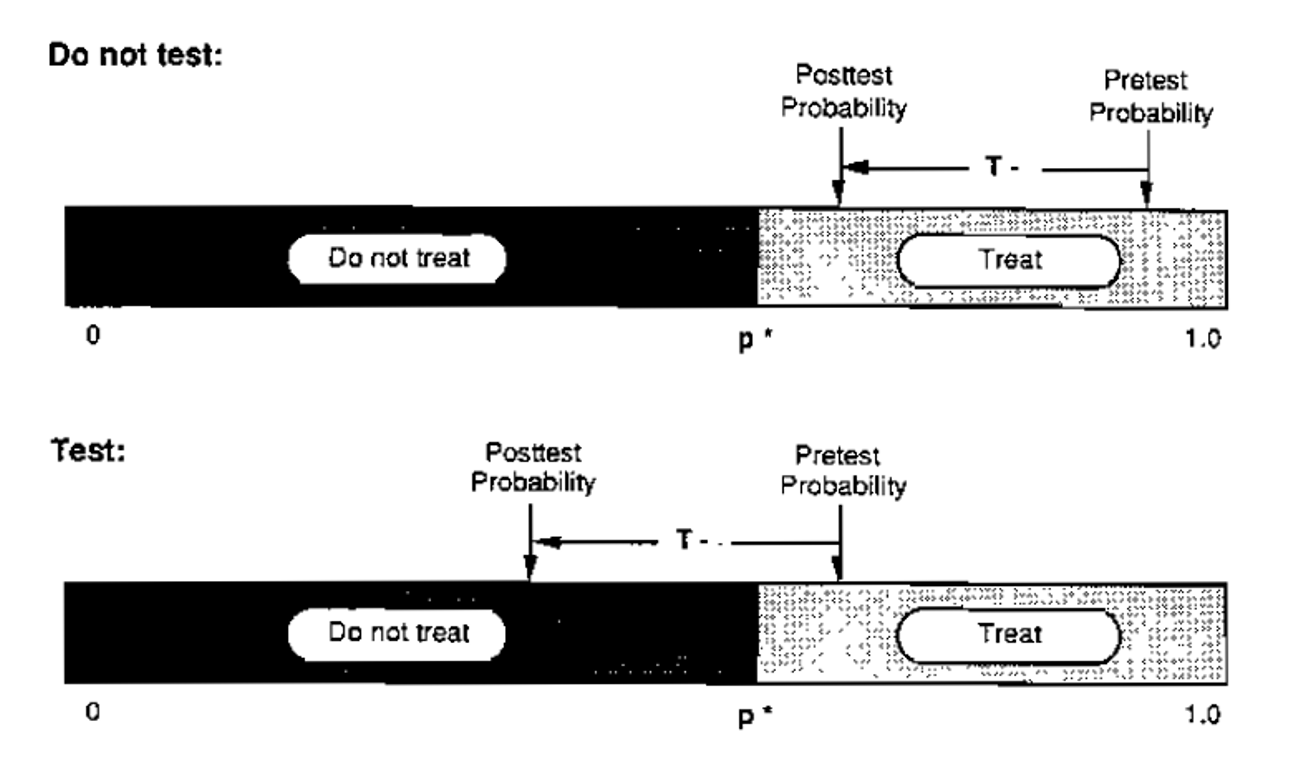
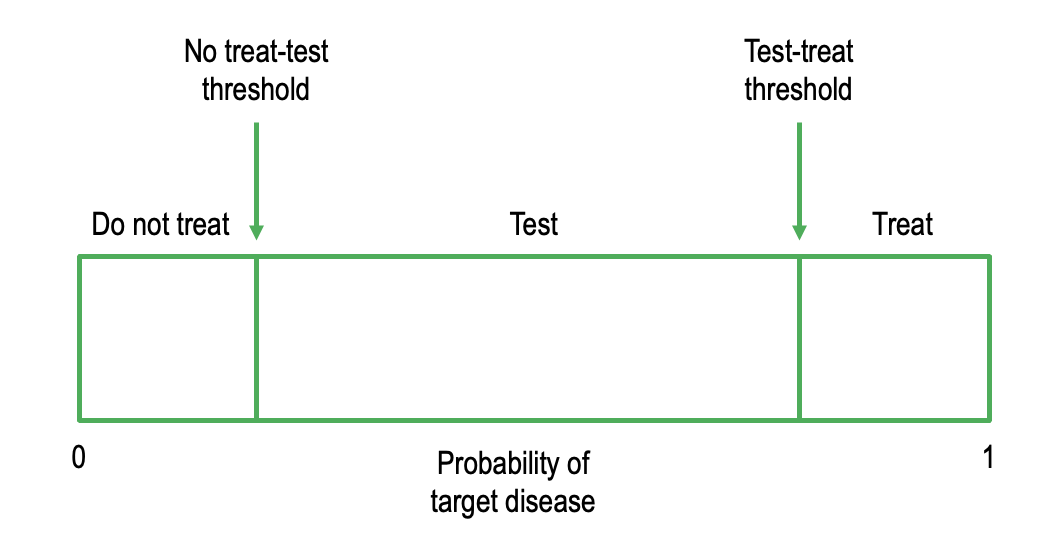
No Treat – Test Threshold
Probability of indifference between testing & not treating

Test – Treat Threshold
Probability of indifference between testing & treatment

Testing & expected value of information

• Information can theoretically be perfect, free, & without risk, but it’s usually NOT!
• Information is almost always IMPERFECT
• Getting information usually HAS A COST

Testing & expected value of information

Value of information asks: what are we gaining by having this extra information?

Value of information =

|[expected value from the ‘gaining information’ strategy] –

[expected value from the next best strategy]|

Testing & expected value of information

PERFECT tests give us an upper limit to the potential benefit from any test

The gain from such an imaginary PERFECT test is the expected value of perfect information (EVPI)

Testing & expected value of information

A perfect test (100% sens and spec) with no risk

A perfect test (100% sens and spec) with no risk

• EV(perfect test) = 0.12

• EV(treat strategy) = 0.16

• EV(no treat strategy) = 0.24 (worst EV)

EVPI =

|EV ‘perfect test’ – EV ‘next best strategy: treat all’|

=|0.12 – 0.16| = 0.04,

or 4 deaths prevented per 100 tests because of the additional testing information

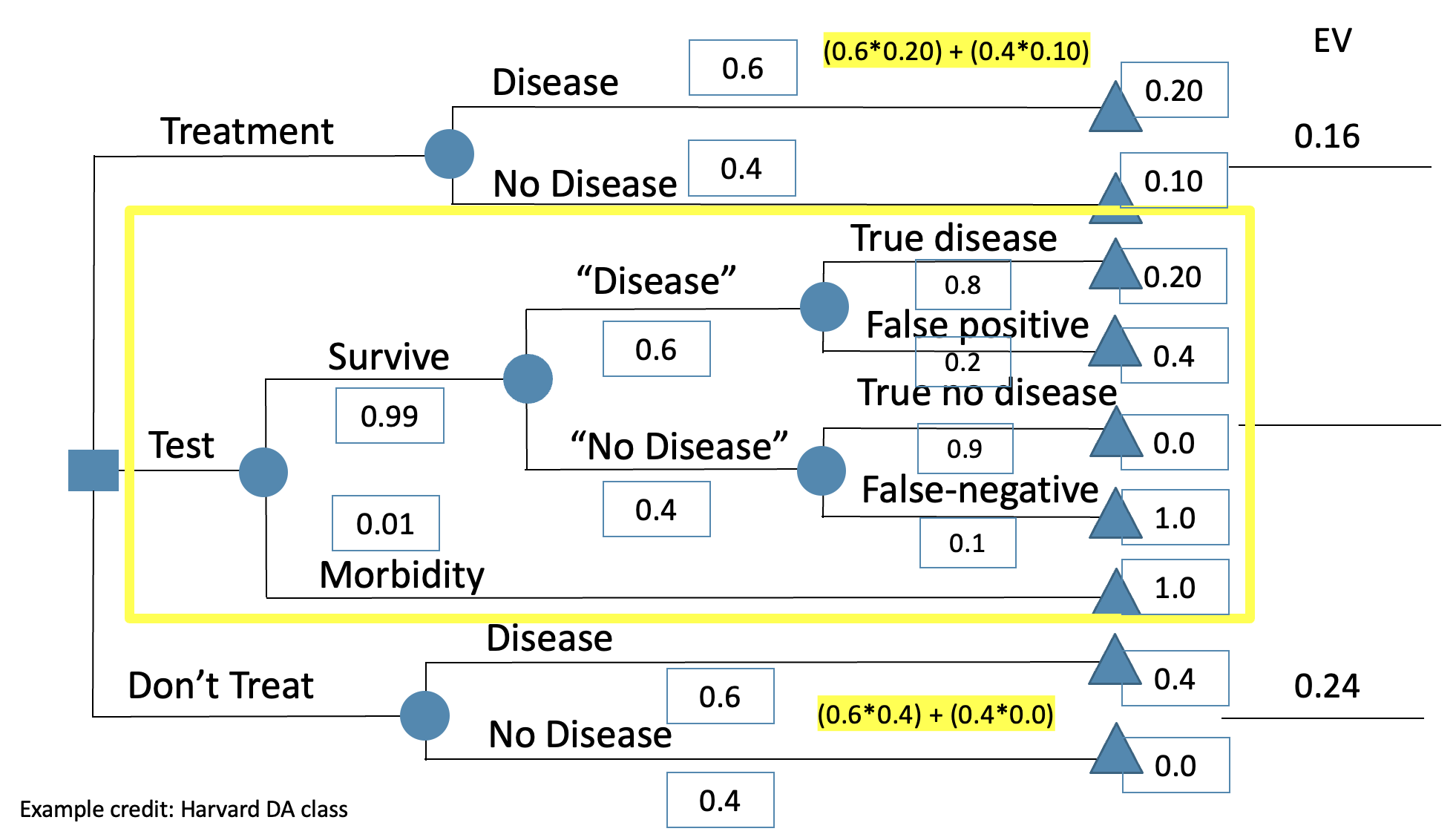
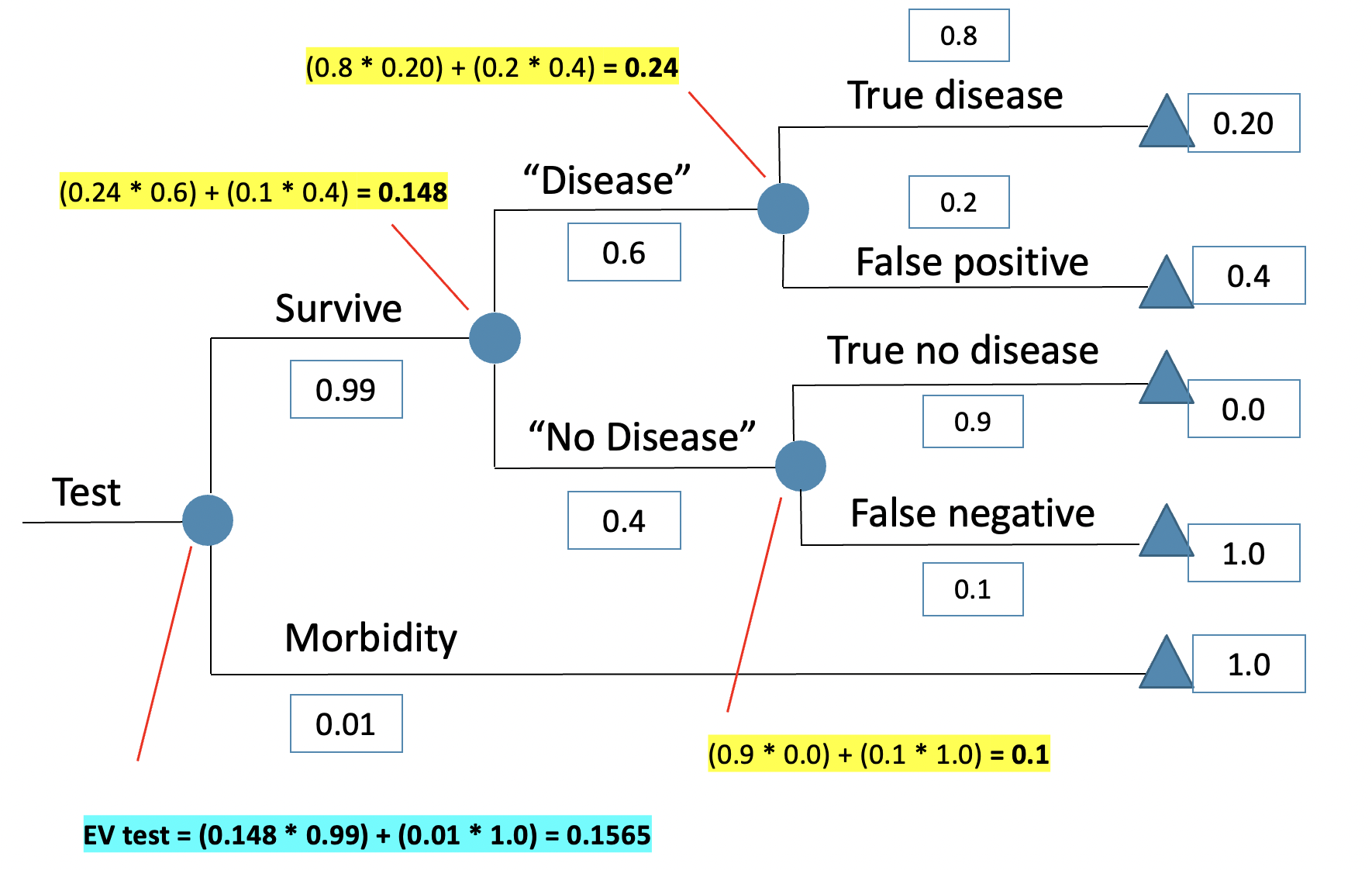
An imperfect test with morbidity risk

An imperfect test with morbidity risk

An imperfect test with morbidity risk

When the test is imperfect, testing is still the best strategy (in this case, the lower EV, the better since our outcome values are the probability of a bad outcome), but not by much:

Testing & expected value of information

When the test is IMPERFECT:

• EV(test strategy) = 0.157

• EV(treat strategy) = 0.16

• EV(no treat strategy) = 0.24 (worst EV)

VOI = |EV ‘test’ – EV ‘next best strategy’|

= |0.157 – 0.16| = 0.003,

or 3 deaths prevented per 1000 tests because of the additional testing information

Next… case studies!