Advanced Modeling Techniques

Learning Objectives and Outline

Learning Objectives

• Be able to understand the basic concepts and identify the strengths and limitations of alternative modeling techniques, including:

  • Microsimulation (Monte Carlo simulation)

  • Discrete event simulation

  • Infectious disease (dynamic) models

Outline

• Microsimulation (Monte Carlo simulation)

• Discrete event simulation

• Infectious disease (dynamic) models

• Comparison of model types

Microsimulation

Microsimulation models

• Markov simulation

  • Focuses on the average: essentially assuming infinite cohort of individuals transitions through the model simultaneously to obtain the expected values

• Microsimulation

  • Synonyms = stochastic microsimulation, individual-based model, 1st order Monte Carlo simulation

  • Hypothetical individuals transition through the model, one at a time

Steps

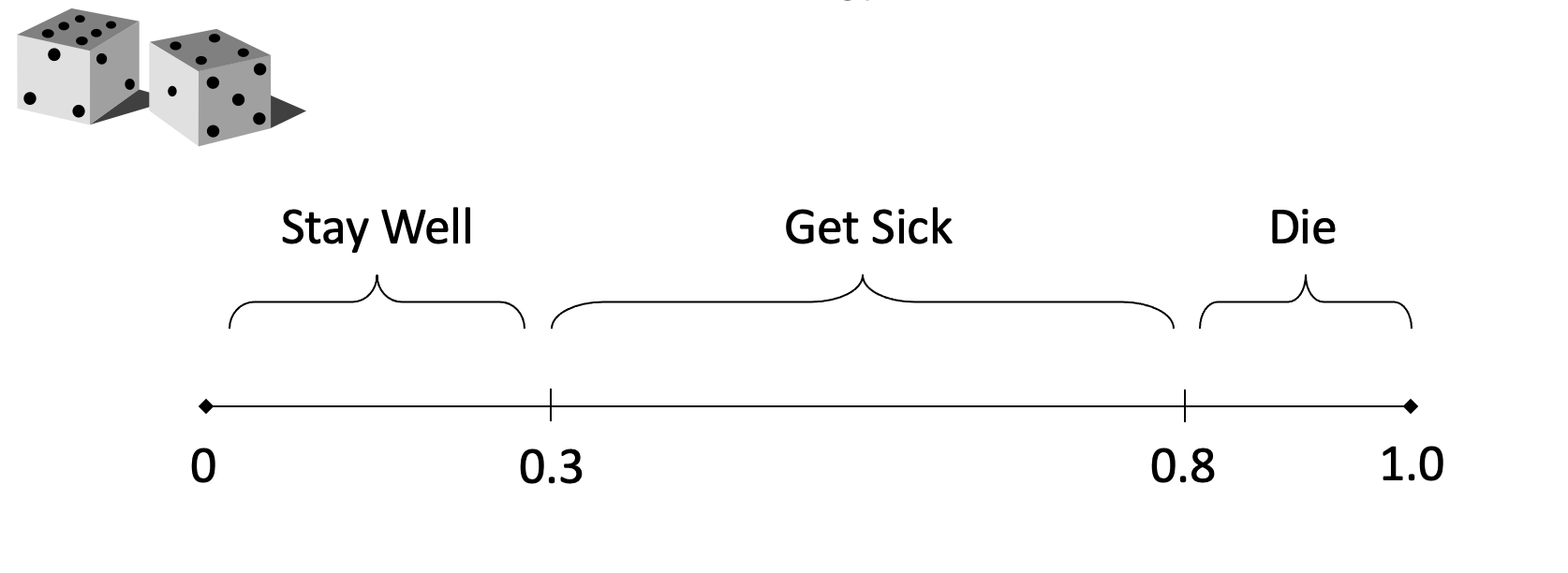
1. Determine initial state, using the distribution of starting probabilities

   • e.g. probability of starting in sick/healthy

2. Simulate individual trajectory through health states, using random numbers to determine actual transitions (yes/no) from transition probabilities

3. Record # of cycles in each state

4. Repeat steps 1-3 many times (N)

Steps

5. Calculate mean # of cycles from sample of N

   • Can weight states by utility, cost, discount factor (same as with Markov models)

Random numbers

Markov cohort vs Microsimulation

[Shift to Powerpoint…]

Example

Context: Economic evaluation of TB prevention among people living with HIV in Tanzania

Zhu et al., The Lancet Global Health, 2022

Example

• TB accounts for >25% deaths among people living with HIV

• Isoniazid preventive therapy (IPT) can prevent TB among people receiving antiretroviral therapy (ART)

• HIV programmes are now initiating patients on ART with higher average CD4 cell counts and lower tuberculosis risks under test-and-treat guidelines

• We aimed to investigate how this change has affected the health impact and cost-effectiveness of IPT

Example

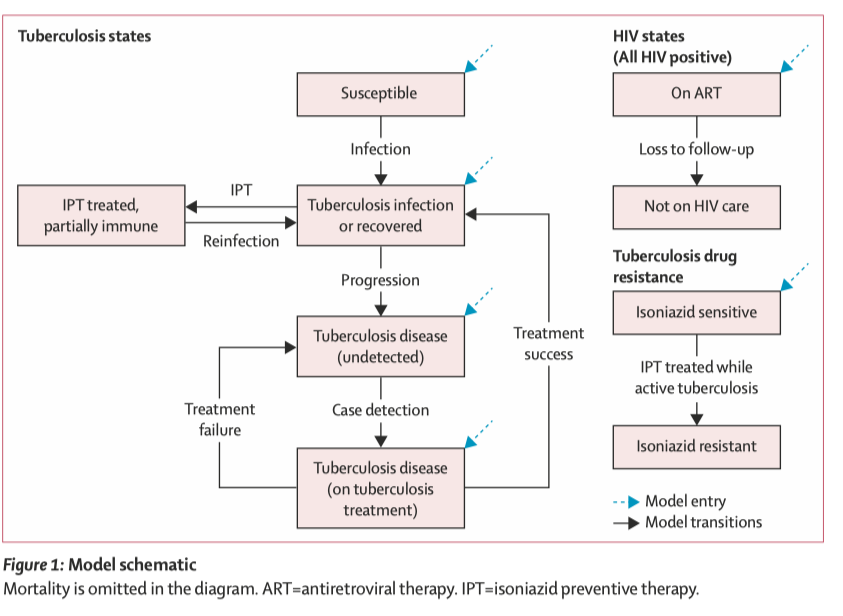
Zhu et al, The Lancet Global Health, 2022

Example

Why choose a microsimulation model?

• Individual-level characteristics on age, sex, CD4 cell count

• Tracking individual trajectory is crucial for this question

  • CD4 cell counts change with HIV treatment

  • Event rates (mortality and TB progression rates) are dependent on CD4 cell counts

• A markov cohort model wouldn’t be able to capture these complex mechanisms!

Discrete event simulation

Microsimulation vs DES

Miscrosimulation

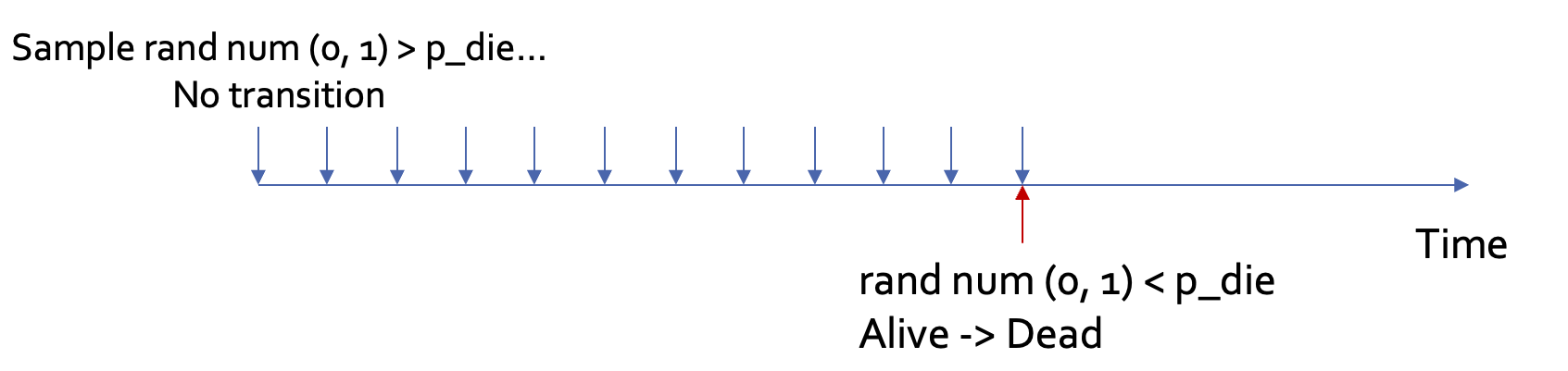
Discrete event simulation

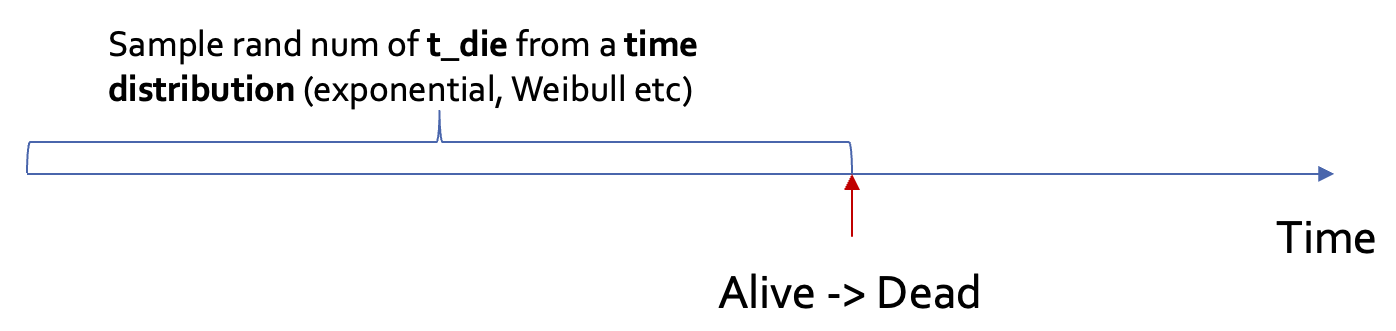
DES

• Similar to microsimulation, DES simulates one individual at a time \rightarrow Subject to stochasticity

• Different from microsimulation (where time is discretized), DES models time continuously

• Pros:

  • Faster: Skips unnecessary cycles where no events happen

  • More natural to implement when data are presented as time-to-event distributions (wait time, length of stay in hospital, onset-to-treatment time for acute conditions)

• Cons:

  • Less intuitive: “time to death is sampled from a Weibull distribution of shape = 2.72, scale = 58.5” (DES) vs. “the probability of death in year 1 is 0.038” (Microsim)

  • Those time steps may be useful even if there’s no event! (In the HIV/TB example, CD4 cell count is updated every cycle to recalculate TB and death risks)

Example

Example

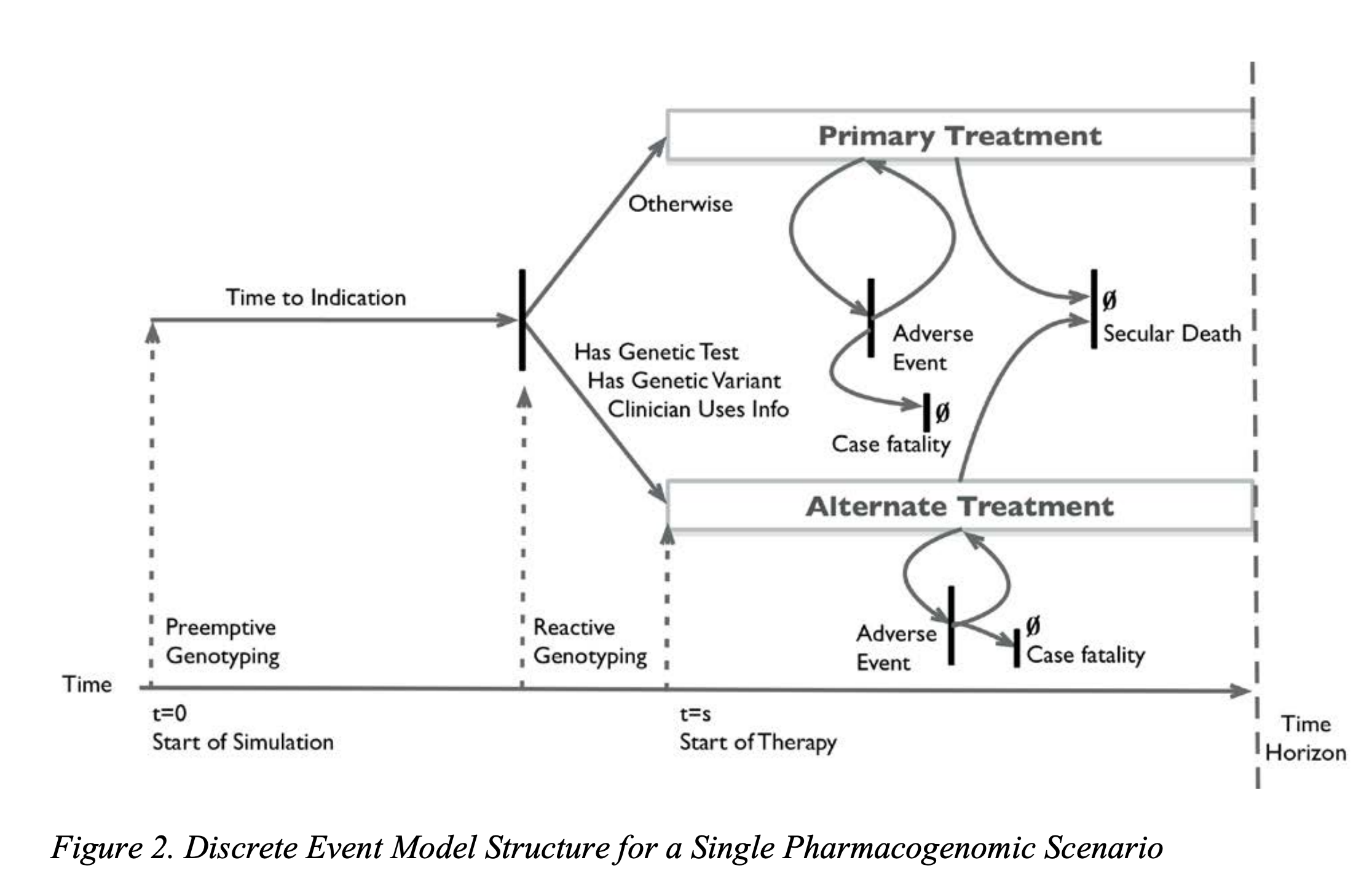
Graves et al, 2017

Infectious disease (dynamic) models

Why dynamic models?

• So far all model types we discussed assume that individuals in the model cohort experience events independently

  • Appropriate assumption for most chronic disease models

• But what about infectious diseases (e.g. COVID) where individuals interact with each other?

  • E.g. the risk of acquiring COVID for a healthy (susceptible) individual depends on how many individuals current have COVID in the population

The SIR model

The most classic model in infectious disease epidemiology. Appropriate for many common infectious diseases (e.g., the flu).

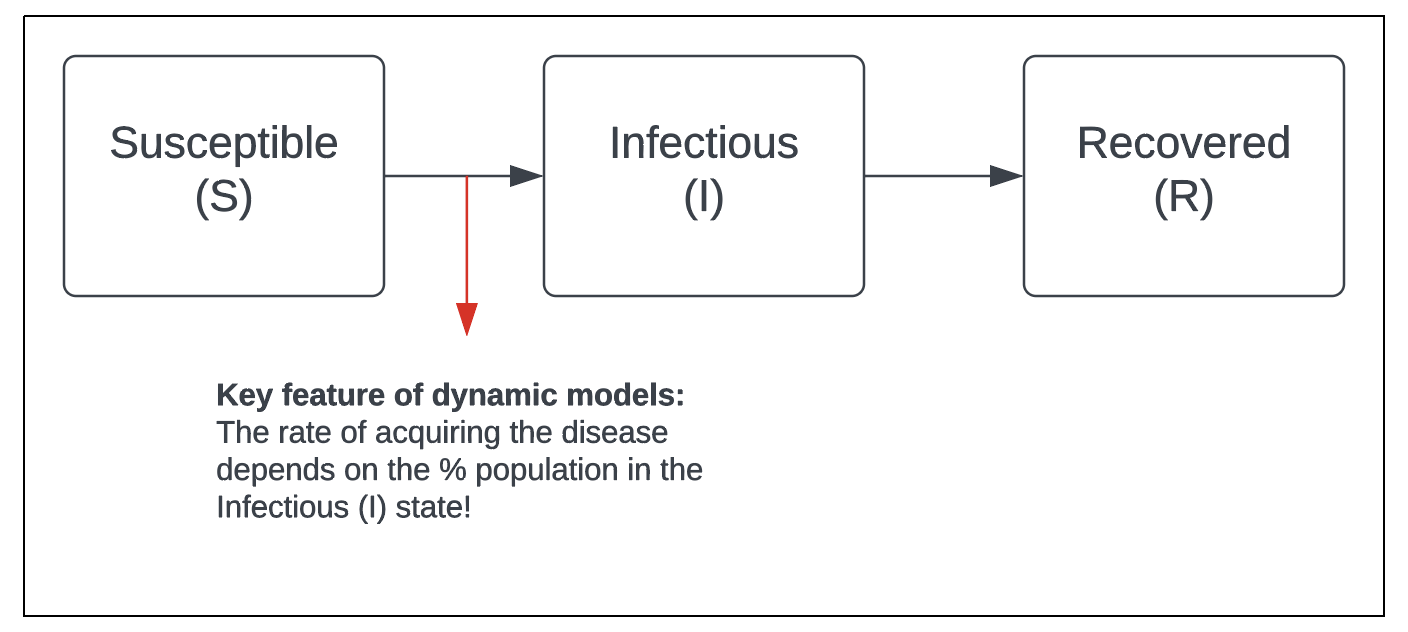
The SIR model

Source: Vynnycky, Emilia; White, Richard. An Introduction to Infectious Disease Modelling.

Variants of the SIR model

• From the simple SIR process, we can add more stuctures to reflect the process of a particular disease, for example:

  • Age- or sex- mixing: appropriate for sexually transmitted diseases

  • A stage where individuals are infected but not infectious: appropriate for diseases with a latent stage, e.g., TB, COVID-19

Dynamic models are often expressed/solved as difference/differential equations

Example:

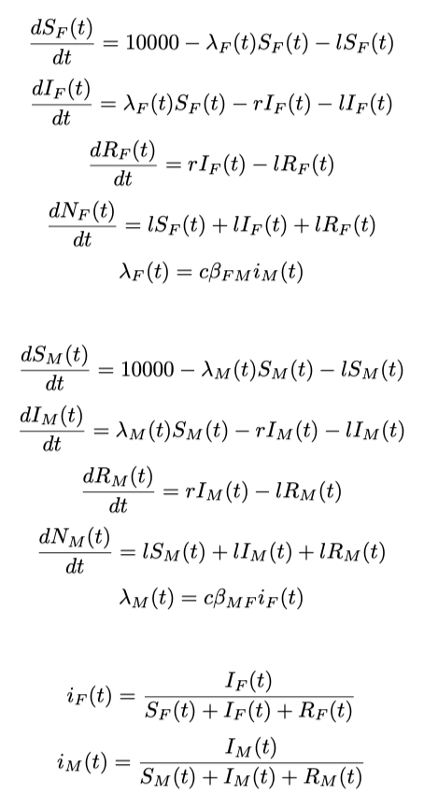
They can be solved by hand or using softwares (e.g. deSolve package in R)

How to choose the right model?

Comparison of model types

Model Type	Strengths	Limitations
Decision tree	Transparent Straightforward calculations	Difficult to capture progression over time or repeated events
Markov cohort	Able to capture repeated events over time Fast run speed	Difficult to capture individual heterogeneity or track history of events Hard to handle complicated disease process (subject to state explosion)

Comparison of model types

Model Type	Strengths	Limitations
Decision tree	Transparent Straightforward calculations	Difficult to capture progression over time or repeated events
Markov cohort	Able to capture repeated events over time Fast run speed	Difficult to capture individual heterogeneity or track history of events Hard to handle complicated disease process (subject to state explosion)
Microsimulation	Easy to track history Very powerful and flexible	Requires a large number of runs to converge Slowest run speed

Comparison of model types

Model Type	Strengths	Limitations
Decision tree	Transparent Straightforward calculations	Difficult to capture progression over time or repeated events
Markov cohort	Able to capture repeated events over time Fast run speed	Difficult to capture individual heterogeneity or track history of events Hard to handle complicated disease process (subject to state explosion)
Microsimulation	Easy to track history Very powerful and flexible	Requires a large number of runs to converge Slowest run speed
Discrete event simulation	Easy to track history Faster than microsimulation	Requires a large number of runs to converge Time-to-event distributions are less intuitive and harder to obtain than event rates/probabilities

Comparison of model types

Model Type	Strengths	Limitations
Decision tree	Transparent Straightforward calculations	Difficult to capture progression over time or repeated events
Markov cohort	Able to capture repeated events over time Fast run speed	Difficult to capture individual heterogeneity or track history of events Hard to handle complicated disease process (subject to state explosion)
Microsimulation	Easy to track history Very powerful and flexible	Requires a large number of runs to converge Slowest run speed
Discrete event simulation	Easy to track history Faster than microsimulation	Requires a large number of runs to converge Time-to-event distributions are less intuitive and harder to obtain than event rates/probabilities
Dynamic	Able to capture transmission of disease	More data requirements (e.g. contact patterns in populaton) More black-box

How to choose the right model?

Factors to consider:

• Policy question/interventions

• Data availability

• Natural history of disease

• Computational resources available