Markov Models

Learning Objectives and Outline

Learning Objectives

• Discuss pros and cons of decision modeling using decision trees vs. a formal deterministic model

• Understand the components and structure of discrete time Markov models

• Calculate Markov cycles by hand, using Markov bubble diagram

• Apply methods for Markov cycle correction

A Simple Disease Process

• Suppose we want to model the cost-effectiveness of alternative strategies to prevent a disease from occurring.
• We start with a healthy population of 25 year olds and there are three health states people can experience:
  1. Remain Healthy
  2. Become Sick
  3. Death

A Simple Disease Process

• Remaining healthy carries no utility decrement (utility weight = 1.0 per cycle in healthy state)
• Becoming sick carries a 0.25 utility decrement for the remainder of the person’s life (utility weight = 0.75)
• Death carries a utility value of 0.

A Simple Disease Process

• There is no cost associated with remaining healthy.
• Becoming sick incurs $1,000 / year in costs.
• Becoming sick increases the risk of death by 300%.

A Simple Disease Process

A country’s health institute is considering five preventive care strategies that reduce the risk of becoming sick:

Strategy	Description	Cost
A	Standard of Care	$25/year
B	Additional 4% reduction in risk of becoming sick	$1,000/year
C	12% reduction in risk	$3,100/year
D	8% reduction in risk	$1,550/year
E	8% reduction in risk	$5,000/year

Model Option 1: Decision Tree

• One option would be to use a decision tree to model the expected utility and costs associated with each strategy.
• Model time horizon: 10 years
• The next slide shows the decision tree for outcomes experienced in the first year.

Model Option 1: Decision Tree

• What limitations do you see?

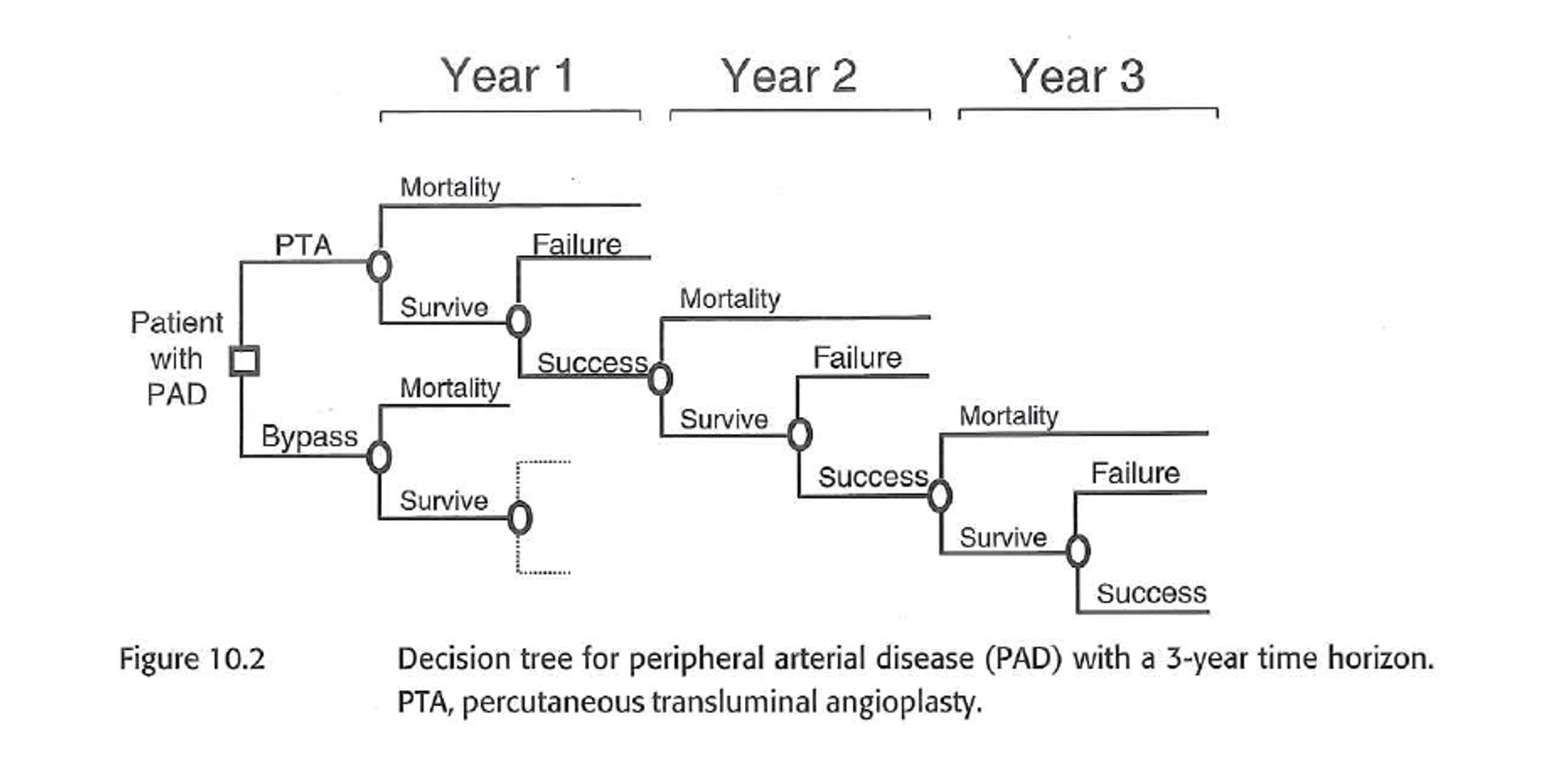
Decision tree for two full cycles.

Strategy A decision tree for 5 cycles.

Decision Trees

Pros	Cons
Simple, rapid & can provide insights

Decision Trees

Pros	Cons
Simple, rapid & can provide insights
Easy to describe & understand

Decision Trees

Pros	Cons
Simple, rapid & can provide insights
Easy to describe & understand
Works well with limited time horizon

Decision Trees

Pros	Cons
Simple, rapid & can provide insights	Difficult to include clinical detail
Easy to describe & understand
Works well with limited time horizon

Decision Trees

Pros	Cons
Simple, rapid & can provide insights	Difficult to include clinical detail
Easy to describe & understand	Elapse of time is not readily evident.
Works well with limited time horizon

Decision Trees

Pros	Cons
Simple, rapid & can provide insights	Difficult to include clinical detail
Easy to describe & understand	Elapse of time is not readily evident.
Works well with limited time horizon	Difficult to model longer (>1 cycle) time horizons

Decision Trees

Next Steps

• Ideally we want a modeling approach that can incorporate flexibility and handle the complexities that make decision trees difficult/unwieldy.

Markov Models

Markov Models

Common approach in decision analyses that adds additional flexibility.

Pros	Cons
Can model repeated events
\quad \quad \quad \quad \quad \quad

Markov Models

Common approach in decision analyses that adds additional flexibility.

Pros	Cons
Can model repeated events
Can model more complex + longitudinal clinical events

Markov Models

Common approach in decision analyses that adds additional flexibility.

Pros	Cons
Can model repeated events
Can model more complex + longitudinal clinical events
Not computationally intensive; efficient to model and debug

Markov Models

• The advantages of Markov models derive from their structure around mutually exclusive disease states.

• These disease states represent the possible states or consequences of strategies or options under consideration.

• Because there are a fixed number of disease states the population can be in, there is no need to model complex pathways, as we saw in the decision tree “explosion” a few slides back.

Markov Trees

It is also common to pair a Markov model with a decision tree.¹

1. Gasauskas et al. 2022

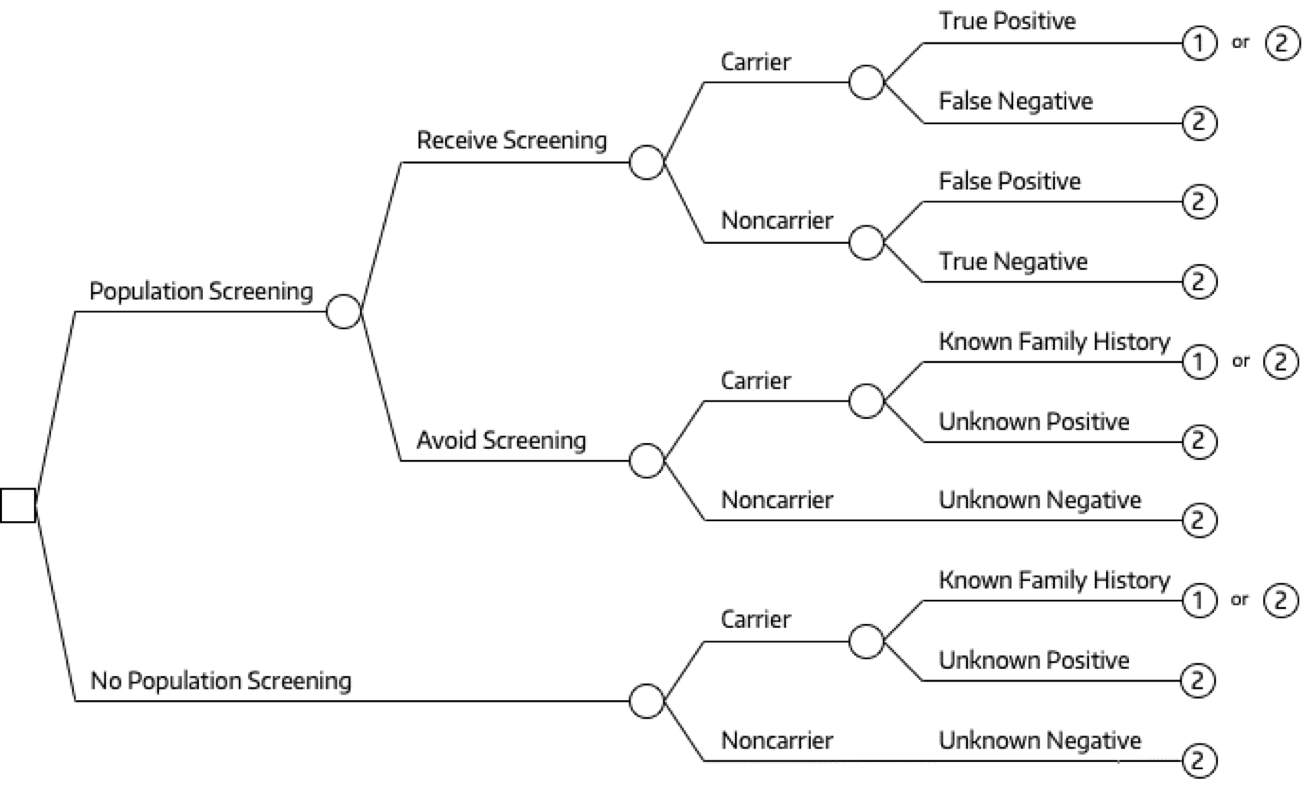
Markov Trees

It is also common to pair a Markov model with a decision tree.¹

1. Gasauskas et al. 2022

Markov Tree

A simple decision tree is implicit in nearly every decision analysis.

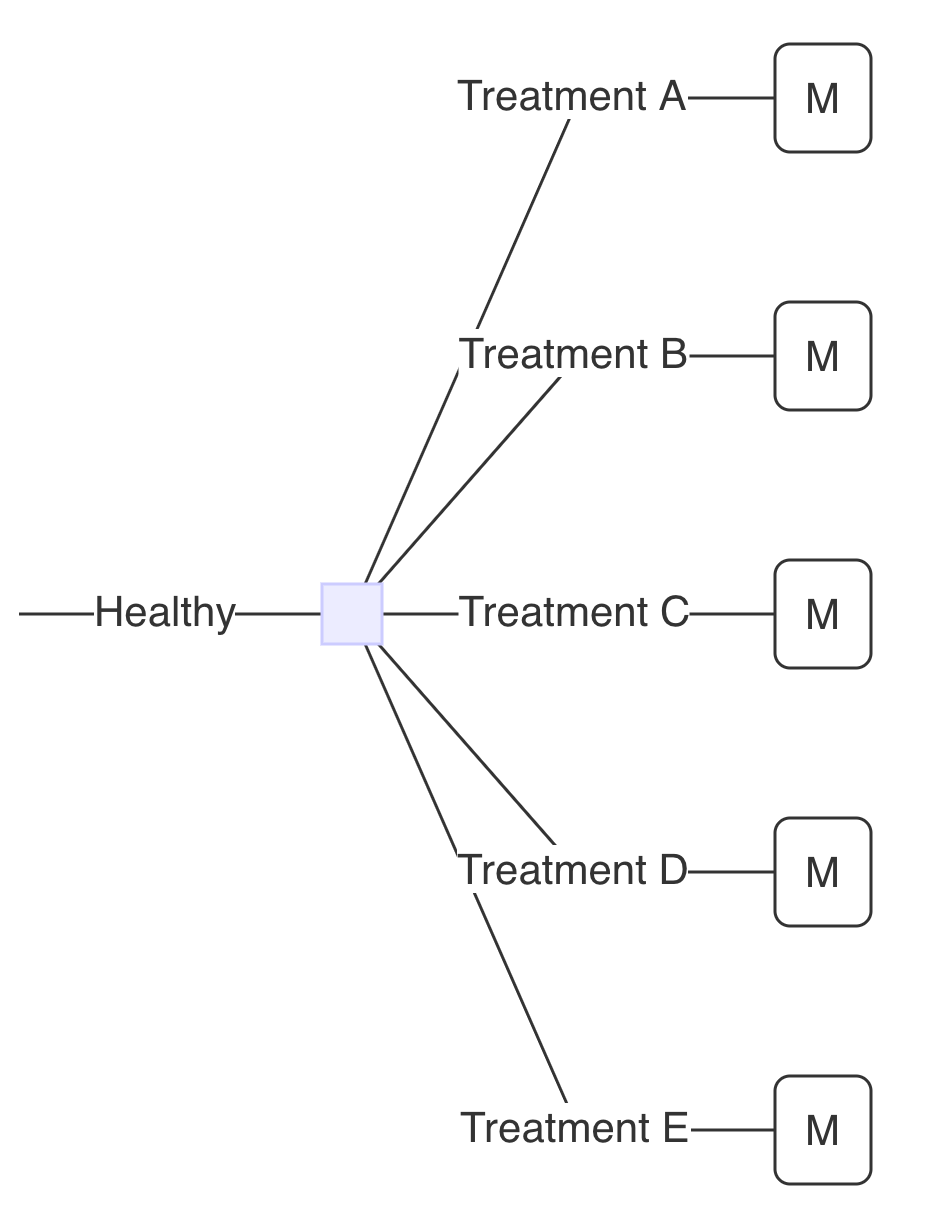
Markov Tree: Example

Treatment A: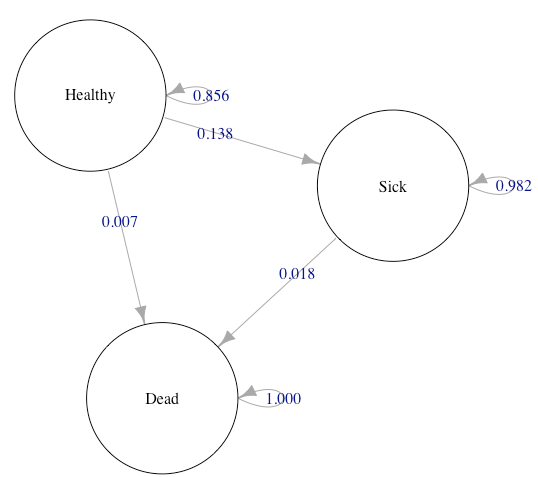

Markov Tree: Example

Treatment A:

When choosing a model structure…

“Things should be made as simple as possible, but not simpler” - Albert Einstein

1. When choosing a model structure, you want to choose one that best fits your research question & one that adequately represents the clinical background/problem – zeroing in on what’s most important

2. You always want to first build the structure completely independently & data free AND then see how hard it is to get data + calibrate

3. You never want to model based on the data* nor do you ever want to make something complicated just to make it complicated**

4. Just because a model is “super complicated/complex” doesn’t mean it’s more publishable or better than something that’s more simplistic

Constructing a Markov Model

Key characteristics

• Allows for health state transitions over time
• Individuals can only exist in one state at a time (mutually exclusive health states)
• At the beginning or end of each cycle, patients transition across health states via transition probabilities & individuals stay in health state for entire cycle length
• Probability of transitioning depends on the current state (“no memory”); (tunnel states can account for this potential limitation)
• Transition probabilities remain constant over time (apart from embedded lifetables)
• Results report “average” of cohort

Key characteristics

“CYCLE” = Minimum amount of time that any individual will spend in a state before possible transition to another state

• More on this in the next slides

Steps

1. Define the decision problem
2. Conceptualize the model
3. Parameterize the model
4. Calculate or define the transition probability matrix
5. Run the model

1. Define the Decision Problem

Step 1: Define the Decision Problem

We defined the decision problem earlier in this lecture, so we’ll repeat the basic objectives briefly here.

Step 1: Define the Decision Problem

Goal: model the cost-effectiveness of alternative strategies to prevent a disease from occurring.

Strategy	Description	Cost
A	Standard of Care	$25/year
B	Additional 4% reduction in risk of becoming sick	$1,000/year
C	12% reduction in risk	$3,100/year
D	8% reduction in risk	$1,550/year
E	8% reduction in risk	$5,000/year

Step 1: Define the Decision Problem

2. Conceptualize the Markov Model

2. Conceptualize the Markov Model

Two major steps:

2a. Determine health states

2b. Determine transitions

Step 2: Conceptualize the Model

2a. Determine health states

• There are three health states people can experience:
  1. Remain Healthy
  2. Become Sick
  3. Death

Step 2: Conceptualize the Model

2a. Determine health states

• There three health states people can experience:
  1. Remain Healthy
  2. Become Sick
  3. Death

2b. Determine transitions

• Individuals who become sick cannot transition back to healthy.

“Bubble Diagram”

State transition (“bubble”) diagrams are useful visualizations of a Markov model.

3. Parameterize the Model

3. Parameterize the Model

Basic steps

3a. Determine basic model parameters

3b. Curate and define model inputs

3. Parameterize the Model

Basic steps

3a. Determine basic model parameters

• Define the population (e.g., 25 year old females)
• Define the Markov cycle length (e.g., 1-year cycle)
• Define the time horizon (e.g., followed until age 100 or death)

3a. Define the Markov Cycle Length

• Fundamentally, we’re modeling a continuous time process (e.g., progression of disease).
• A discrete time Markov model “breaks up” time into “chunks” (i.e., “cycles”).
• A consequence is that the model will show us what fraction start out a cycle in a given state, and what fraction end up in each state at the end of the cycle.

3a. Define the Markov cycle length

• Suppose we used a one-year cycle for the healthy-sick-dead model.
• Think about the underlying (continuous time) disease process.
  • Recall that becoming sick substantially increases the likelihood of death.
• If we’re not careful, what are we (implicitly) assuming can and can’t happen in a single cycle?

3a. Define the Markov Cycle Length

3a. Define the Markov Cycle Length

The challenge of selecting an appropriate cycle length boils down to how we deal with competing risks.

• Competing risks: individuals can transition from their current health state to two or more other health states.

3a. Define the Markov Cycle Length

The challenge of selecting an appropriate cycle length boils down to how we deal with competing risks.

• If we’re not careful, we could effectively rule out the possibility of Healthy Sick Dead within a cycle.
• The model would look like a basic Healthy Dead transition, but they took a detour through Sick along the way!

3a. Define the Markov Cycle Length

Pros	Cons
Can model repeated events	Competing risks are a challenge
Can model more complex + longitudinal clinical events
Not computationally intensive; efficient to model and debug

3a. Define the Markov Cycle Length

• It may be tempting to simply shorten the cycle length (e.g., use 1 day cycle vs. 1 year cycle).

• For a 75 year horizon, how many cycles would that be?
  • 27,375!!!
• Any possible issues with this?

3a. Define the Markov Cycle Length

• Shortening the cycle creates a computational challenge.

• Base case requires 27,375 daily cycles.
• Now suppose we want to run 2,000 probabilistic sensitivity analysis model runs.
  • We now have 57,750,000 cycle runs to contend with!

3a. Define the Markov Cycle Length

Pros	Cons
Can model repeated events	Can only transition once in a given cycle
Can model more complex + longitudinal clinical events	Shortening the cycle can create computational challenges.
Not computationally intensive; efficient to model and debug

3a. Define the Markov Cycle Length

More challenges …

3a. Define the Markov Cycle Length

More challenges …

• Markov models are “memoryless” – they don’t remember what happened before the current cycle.
  • If your risk of transition to a sicker health state depends on events that happened earlier in time, the model can’t explicitly account for this.

3a. Define the Markov Cycle Length

More challenges …

• There are workarounds known as “tunnel states” to get around this problem, though these are difficult to do and present their own challenges
  • We won’t cover them this week but we can provide references if you want to explore!

3a. Define the Markov Cycle Length

Pros	Cons
Can model repeated events	Can only transition once in a given cycle
Can model more complex + longitudinal clinical events	Shortening the cycle can create computational challenges.
Not computationally intensive; efficient to model and debug	Shortening cycle can cause “state explosion” if tunnel states are used

3a. Define the Markov Cycle Length

• It’s also advisable to pick a cycle length that aligns with the clinical/disease timelines of the decision problem.
  • Treatment schedules.
  • Acute vs. chronic condition.
• Another option is to incorporate “short-run” events that happen early in the course of a disease/intervention within the decision tree, then allow the Markov model to model longer-term health consequences.

3. Parameterize the Model

3b. Curate and define model inputs

• 3b.i. Source and define the base case values.

• 3b.ii. Source and define sources of uncertainty.

3. Parameterize the Model

3b. Curate and define model inputs

• Rate of disease onset
• Health state utilities and costs
• Hazard ratios, odds ratios or relative risks for different strategies.
• … and so on.

3. Parameterize the Model

We defined many of the underlying parameters earlier in this lecture, so we’ll repeat them briefly here.

3. Parameterize the Model

• We start with a healthy population of 25 year olds and follow them until age 100 (or death, if earlier).

• Remaining healthy carries no utility decrement (utility weight= 1.0)
• Becoming sick carries a 0.25 utility decrement for the remainder of the person’s life (utility weight = 0.75)
• Death carries a utility weight value of 0.

3. Parameterize the Model

• There is no cost associated with remaining healthy.

• Becoming sick incurs $1,000 / year in costs.
• Becoming sick increases the risk of death by 300%.

3. Parameterize the Model

Each strategy has a different cost and impact on the likelihood of becoming sick.

Strategy	Description	Cost
A	Standard of Care	$25/year
B	Additional 4% reduction in risk of becoming sick	$1,000/year
C	12% reduction in risk	$3,100/year
D	8% reduction in risk	$1,550/year
E	8% reduction in risk	$5,000/year

3. Parameterize the Model

It is critical to follow a formal process for parameterizing your model.

• Often, parameters are drawn from the published literature, and it is important to track the source (published value, assumption, etc.) for each model parameter.
  • For example, the percent risk reduction parameter for each strategy may come from different clinical trials.
  • The parameter governing death from background causes may be derived from mortality data.

3. Parameterize the Model

It is critical to follow a formal process for parameterizing your model.

• Some parameters may just be values (e.g., cost of Strategy A is $25/yr)
• Some parameters may be functions of other parameters.
  • For example, suppose we want to follow a cohort of 25 year olds until age 100 or death, if it occurs earlier.
  • In that case we have two “fixed” parameters: the starting age, and the maximum age.
  • We can use these two parameters to infer the total number of cycles we need to run.

3. Parameterize the Model

It is critical to follow a formal process for parameterizing your model.

• Parameters also have various “flavors”:
  1. Probabilities
  2. Rates
  3. Hazard ratios
  4. Costs
  5. Utilities
  6. etc.

3. Parameterize the Model

It is critical to follow a formal process for parameterizing your model.

• All of the above highlight the importance of adopting a formal process for naming and tracking the value, source, and uncertainty distribution of all model parameters in one place.

• We recommend a structured approach based on parameter naming conventions and parameter tables.

3. Parameterize the Model

Naming conventions:

type	prefix
Probability	p_
Rate	r_
Matrix	m_
Cost	c_
Utility	u_
Hazard Ratio	hr_

Parameter Table

Parameter Table
param	base_case	formula	description	notes	distribution	source
n_age_init	25.00		Age at baseline			Modeling Parameter
n_age_max	100.00		Maximum age of followup			Modeling Parameter
u_H	1.00		Utility weight of healthy (H)		beta(shape1 = 200, shape2 = 3)	Leech et al. (2022)
u_S	0.75		Utility weight of sick (S)		beta(shape1 = 130, shape2 = 45)	Leech et al. (2022)
c_S	1000.00		Annual cost of sick (S)		gamma(shape = 44.4, scale = 22.5)	Graves et al. (2022)
c_trtA	25.00		Cost of treatment A		gamma(shape = 12.5, scale = 2)	Martin et al. (2022)
c_trtB	1000.00		Cost of treatment B		gamma(shape = 12, scale = 83.3)	Assumption
c_trtC	3100.00		Cost of treatment C		gamma(shape = 36.144, scale = 83)	Assumption
n_cycles	75.00	(n_age_max - n_age_init)	Time horizon

param column is the short name of the parameter

Parameter Table
param	base_case	formula	description	notes	distribution	source
n_age_init	25.00		Age at baseline			Modeling Parameter
n_age_max	100.00		Maximum age of followup			Modeling Parameter
u_H	1.00		Utility weight of healthy (H)		beta(shape1 = 200, shape2 = 3)	Leech et al. (2022)
u_S	0.75		Utility weight of sick (S)		beta(shape1 = 130, shape2 = 45)	Leech et al. (2022)
c_S	1000.00		Annual cost of sick (S)		gamma(shape = 44.4, scale = 22.5)	Graves et al. (2022)
c_trtA	25.00		Cost of treatment A		gamma(shape = 12.5, scale = 2)	Martin et al. (2022)
c_trtB	1000.00		Cost of treatment B		gamma(shape = 12, scale = 83.3)	Assumption
c_trtC	3100.00		Cost of treatment C		gamma(shape = 36.144, scale = 83)	Assumption
n_cycles	75.00	(n_age_max - n_age_init)	Time horizon

base_case is the parameter value for the base case.

Parameter Table
param	base_case	formula	description	notes	distribution	source
n_age_init	25.00		Age at baseline			Modeling Parameter
n_age_max	100.00		Maximum age of followup			Modeling Parameter
u_H	1.00		Utility weight of healthy (H)		beta(shape1 = 200, shape2 = 3)	Leech et al. (2022)
u_S	0.75		Utility weight of sick (S)		beta(shape1 = 130, shape2 = 45)	Leech et al. (2022)
c_S	1000.00		Annual cost of sick (S)		gamma(shape = 44.4, scale = 22.5)	Graves et al. (2022)
c_trtA	25.00		Cost of treatment A		gamma(shape = 12.5, scale = 2)	Martin et al. (2022)
c_trtB	1000.00		Cost of treatment B		gamma(shape = 12, scale = 83.3)	Assumption
c_trtC	3100.00		Cost of treatment C		gamma(shape = 36.144, scale = 83)	Assumption
n_cycles	75.00	(n_age_max - n_age_init)	Time horizon

formula defines model parameter formulas for parameters that are functions of other model parameters.

Parameter Table
param	base_case	formula	description	notes	distribution	source
n_age_init	25.00		Age at baseline			Modeling Parameter
n_age_max	100.00		Maximum age of followup			Modeling Parameter
u_H	1.00		Utility weight of healthy (H)		beta(shape1 = 200, shape2 = 3)	Leech et al. (2022)
u_S	0.75		Utility weight of sick (S)		beta(shape1 = 130, shape2 = 45)	Leech et al. (2022)
c_S	1000.00		Annual cost of sick (S)		gamma(shape = 44.4, scale = 22.5)	Graves et al. (2022)
c_trtA	25.00		Cost of treatment A		gamma(shape = 12.5, scale = 2)	Martin et al. (2022)
c_trtB	1000.00		Cost of treatment B		gamma(shape = 12, scale = 83.3)	Assumption
c_trtC	3100.00		Cost of treatment C		gamma(shape = 36.144, scale = 83)	Assumption
n_cycles	75.00	(n_age_max - n_age_init)	Time horizon

description provides a text description of the parameter.

Parameter Table
param	base_case	formula	description	notes	distribution	source
n_age_init	25.00		Age at baseline			Modeling Parameter
n_age_max	100.00		Maximum age of followup			Modeling Parameter
u_H	1.00		Utility weight of healthy (H)		beta(shape1 = 200, shape2 = 3)	Leech et al. (2022)
u_S	0.75		Utility weight of sick (S)		beta(shape1 = 130, shape2 = 45)	Leech et al. (2022)
c_S	1000.00		Annual cost of sick (S)		gamma(shape = 44.4, scale = 22.5)	Graves et al. (2022)
c_trtA	25.00		Cost of treatment A		gamma(shape = 12.5, scale = 2)	Martin et al. (2022)
c_trtB	1000.00		Cost of treatment B		gamma(shape = 12, scale = 83.3)	Assumption
c_trtC	3100.00		Cost of treatment C		gamma(shape = 36.144, scale = 83)	Assumption
n_cycles	75.00	(n_age_max - n_age_init)	Time horizon

notes is an optional column where you add additional notes or context for the parameter.

Parameter Table
param	base_case	formula	description	notes	distribution	source
n_age_init	25.00		Age at baseline			Modeling Parameter
n_age_max	100.00		Maximum age of followup			Modeling Parameter
u_H	1.00		Utility weight of healthy (H)		beta(shape1 = 200, shape2 = 3)	Leech et al. (2022)
u_S	0.75		Utility weight of sick (S)		beta(shape1 = 130, shape2 = 45)	Leech et al. (2022)
c_S	1000.00		Annual cost of sick (S)		gamma(shape = 44.4, scale = 22.5)	Graves et al. (2022)
c_trtA	25.00		Cost of treatment A		gamma(shape = 12.5, scale = 2)	Martin et al. (2022)
c_trtB	1000.00		Cost of treatment B		gamma(shape = 12, scale = 83.3)	Assumption
c_trtC	3100.00		Cost of treatment C		gamma(shape = 36.144, scale = 83)	Assumption
n_cycles	75.00	(n_age_max - n_age_init)	Time horizon

distribution specifies the uncertainty distribution for the parameter. It is used for probabilistic sensitivity analyses, which we cover in our intermediate (week-long) workshop.

Parameter Table
param	base_case	formula	description	notes	distribution	source
n_age_init	25.00		Age at baseline			Modeling Parameter
n_age_max	100.00		Maximum age of followup			Modeling Parameter
u_H	1.00		Utility weight of healthy (H)		beta(shape1 = 200, shape2 = 3)	Leech et al. (2022)
u_S	0.75		Utility weight of sick (S)		beta(shape1 = 130, shape2 = 45)	Leech et al. (2022)
c_S	1000.00		Annual cost of sick (S)		gamma(shape = 44.4, scale = 22.5)	Graves et al. (2022)
c_trtA	25.00		Cost of treatment A		gamma(shape = 12.5, scale = 2)	Martin et al. (2022)
c_trtB	1000.00		Cost of treatment B		gamma(shape = 12, scale = 83.3)	Assumption
c_trtC	3100.00		Cost of treatment C		gamma(shape = 36.144, scale = 83)	Assumption
n_cycles	75.00	(n_age_max - n_age_init)	Time horizon

source provides the source for the parameter. It could be a published research article, an assumption, or just simply an unsourced modeling parameter (e.g., the starting age of the modeled cohort).

Parameter Table
param	base_case	formula	description	notes	distribution	source
n_age_init	25.00		Age at baseline			Modeling Parameter
n_age_max	100.00		Maximum age of followup			Modeling Parameter
u_H	1.00		Utility weight of healthy (H)		beta(shape1 = 200, shape2 = 3)	Leech et al. (2022)
u_S	0.75		Utility weight of sick (S)		beta(shape1 = 130, shape2 = 45)	Leech et al. (2022)
c_S	1000.00		Annual cost of sick (S)		gamma(shape = 44.4, scale = 22.5)	Graves et al. (2022)
c_trtA	25.00		Cost of treatment A		gamma(shape = 12.5, scale = 2)	Martin et al. (2022)
c_trtB	1000.00		Cost of treatment B		gamma(shape = 12, scale = 83.3)	Assumption
c_trtC	3100.00		Cost of treatment C		gamma(shape = 36.144, scale = 83)	Assumption
n_cycles	75.00	(n_age_max - n_age_init)	Time horizon

4. Calculate or define the transition probability matrix

Defining the Transition Probability Matrix

• The transition probability matrix is a square matrix that defines the probability of transitioning from one health state to another health state in a single time step.

• Constructing the matrix is a fairly technical, but fairly straightforward process.

  • We will skip over this process for now, but come back to it later today!

Transition Probability Matrix

	Healthy	Sick	Dead
Healthy	0.856	0.138	0.007
Sick	0	0.982	0.018
Dead	0	0	1

5. Run the Model

Executing the model requires two inputs

Health State Occupancy at Beginning of Cycle

Transition Probability Matrix

Health State Occupancy at Beginning of Cycle

Transition Probability Matrix

Health State Occupancy at Beginning of Cycle

Transition Probability Matrix

\quad \quad \quad \quad \quad \quad \quad \quad

s =

 H S D
 1 0 0

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

\quad \quad \quad \quad

Health State Occupancy at Beginning of Cycle

Transition Probability Matrix

Health State Occupancy at End of Cycle

s =

 H S D
 1 0 0

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

s \cdot P=

     H     S     D
 0.856 0.138 0.007

Health State Occupancy at Beginning of Cycle

Transition Probability Matrix

Health State Occupancy at End of Cycle

s =

 H S D
 1 0 0

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

s \cdot P=

     H     S     D
 0.856 0.138 0.007

Health State Occupancy at Beginning of Cycle

Transition Probability Matrix

Health State Occupancy at End of Cycle

s =

 H S D
 1 0 0

     H     S     D
 0.856 0.138 0.007

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

s \cdot P=

     H     S     D
 0.856 0.138 0.007

     H     S     D
 0.733 0.254 0.015

Health State Occupancy at Beginning of Cycle

Transition Probability Matrix

Health State Occupancy at End of Cycle

s =

 H S D
 1 0 0

     H     S     D
 0.856 0.138 0.007

     H     S     D
 0.733 0.254 0.015

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

s \cdot P=

     H     S     D
 0.856 0.138 0.007

     H     S     D
 0.733 0.254 0.015

     H    S     D
 0.627 0.35 0.025

Health State Occupancy at End of Cycle

     H     S     D
 0.856 0.138 0.007

       H       S        D
 0.73274 0.25364 0.015476

       H      S        D
 0.62722 0.3502 0.025171

Markov Trace

Health State Occupancy Over Ten Cycles

 cycle       H       S        D
     0 1.00000 0.00000 0.000000
     1 0.85600 0.13800 0.007000
     2 0.73274 0.25364 0.015476
     3 0.62722 0.35020 0.025171
     4 0.53690 0.43045 0.035865
     5 0.45959 0.49679 0.047371
     6 0.39341 0.55127 0.059531
     7 0.33676 0.59564 0.072207
     8 0.28826 0.63139 0.085286
     9 0.24675 0.65981 0.098669
    10 0.21122 0.68198 0.112273

Calculate cycles by hand

In-class example

• A new drug was developed for cancer patients in remission to decrease their chance of relapse
• This drug is $10,000 per year (2022 USD)
• Research question: Is the new drug cost-effective compared to the current standard of care?
• Let’s say we want to model this over a 4-year time horizon

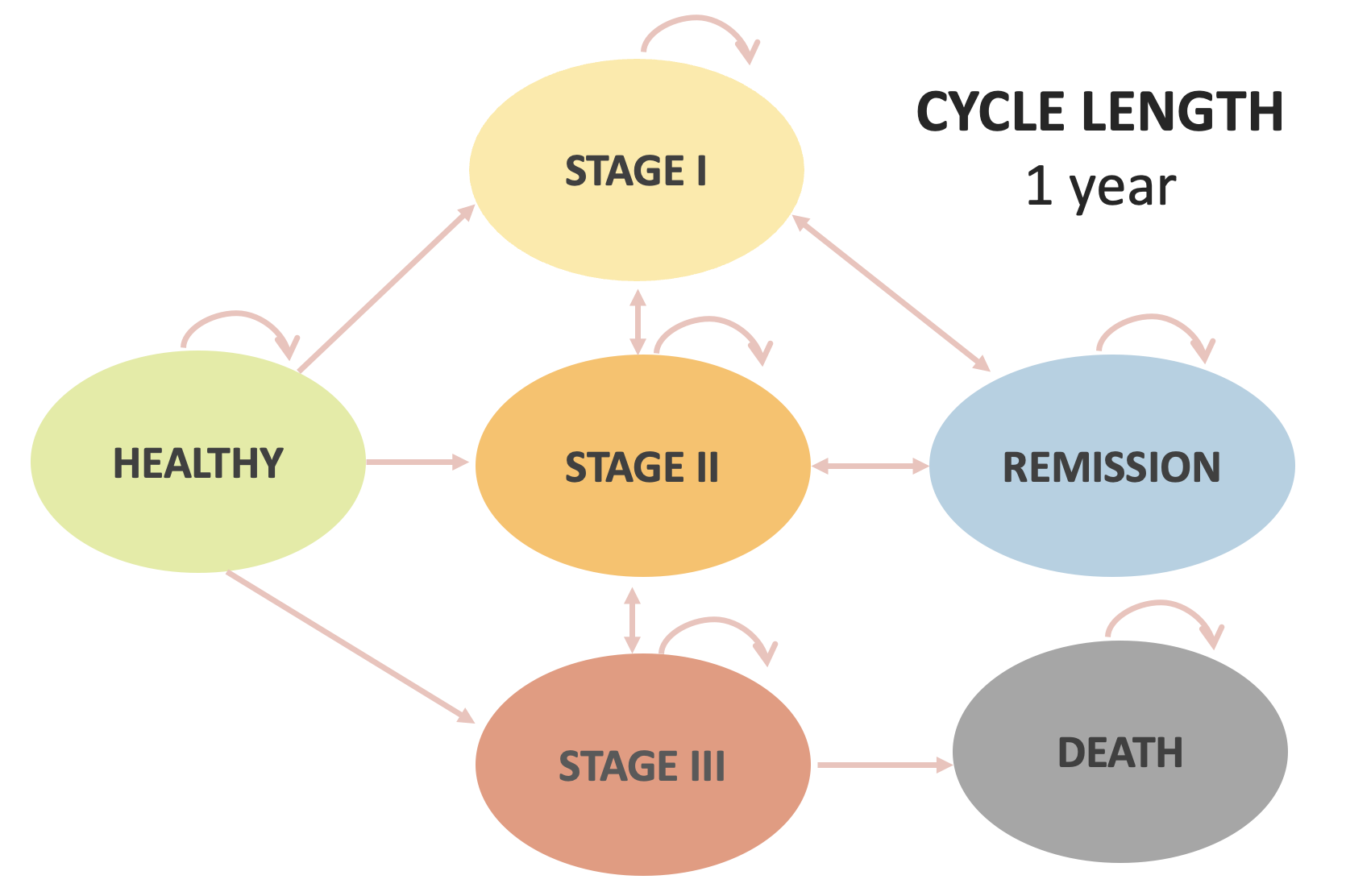
In-class example

	Standard of Care	New Drug
Healthy to Stage 1	5%
Healthy to Stage 2	2%
Healthy to Stage 3	1%
Stage 1 to Stage 2	10%
Stage 1 to Remission	25%
Stage 2 to Stage 1	5%
Stage 2 to Stage 3	15%
Stage 2 to Remission	20%
Stage 3 to Stage 2	5%
Stage 3 to Death	45%
Remission to Stage 1	10%	2%
Remission to Stage 2	5%	1%

In-class example

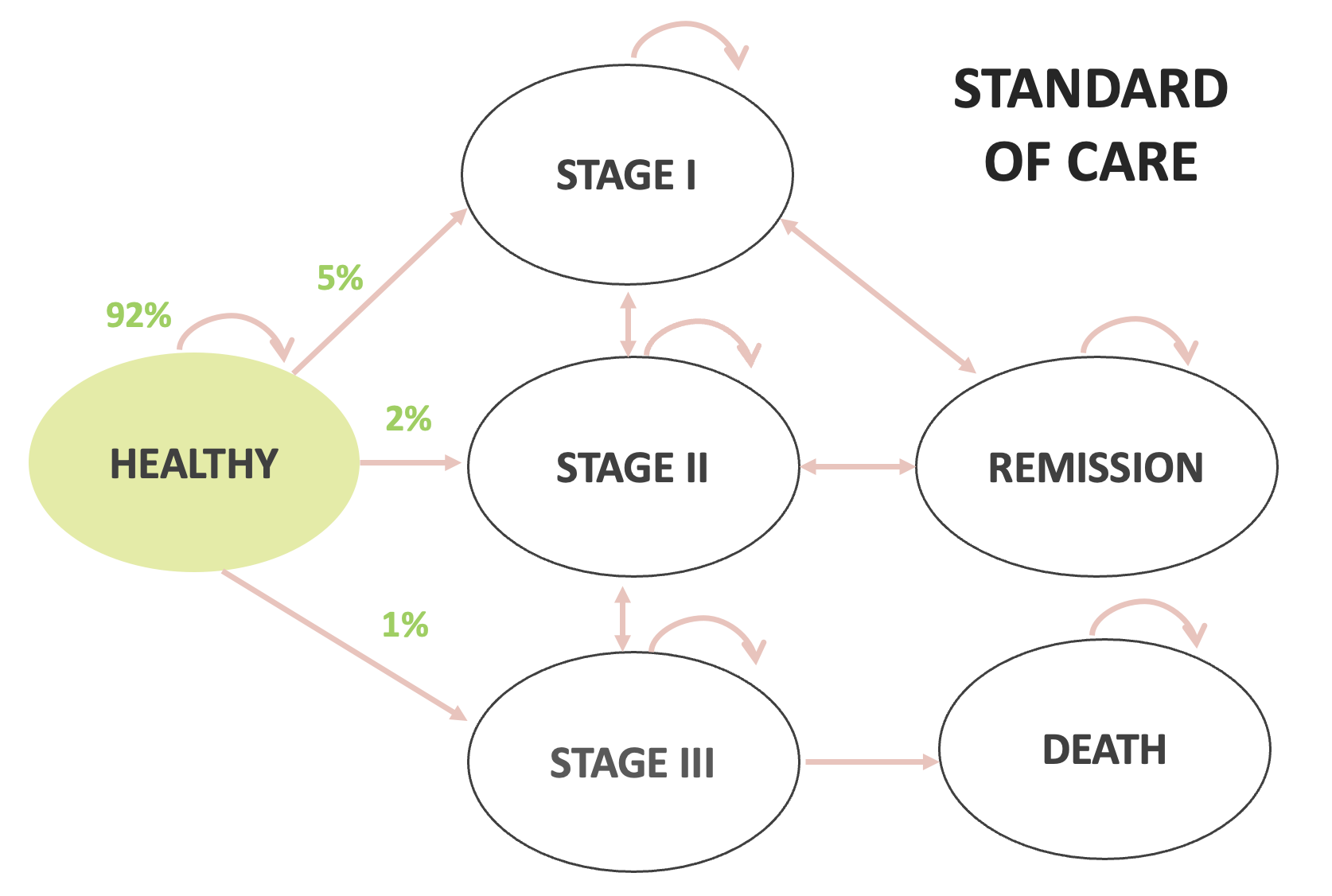
In-class example

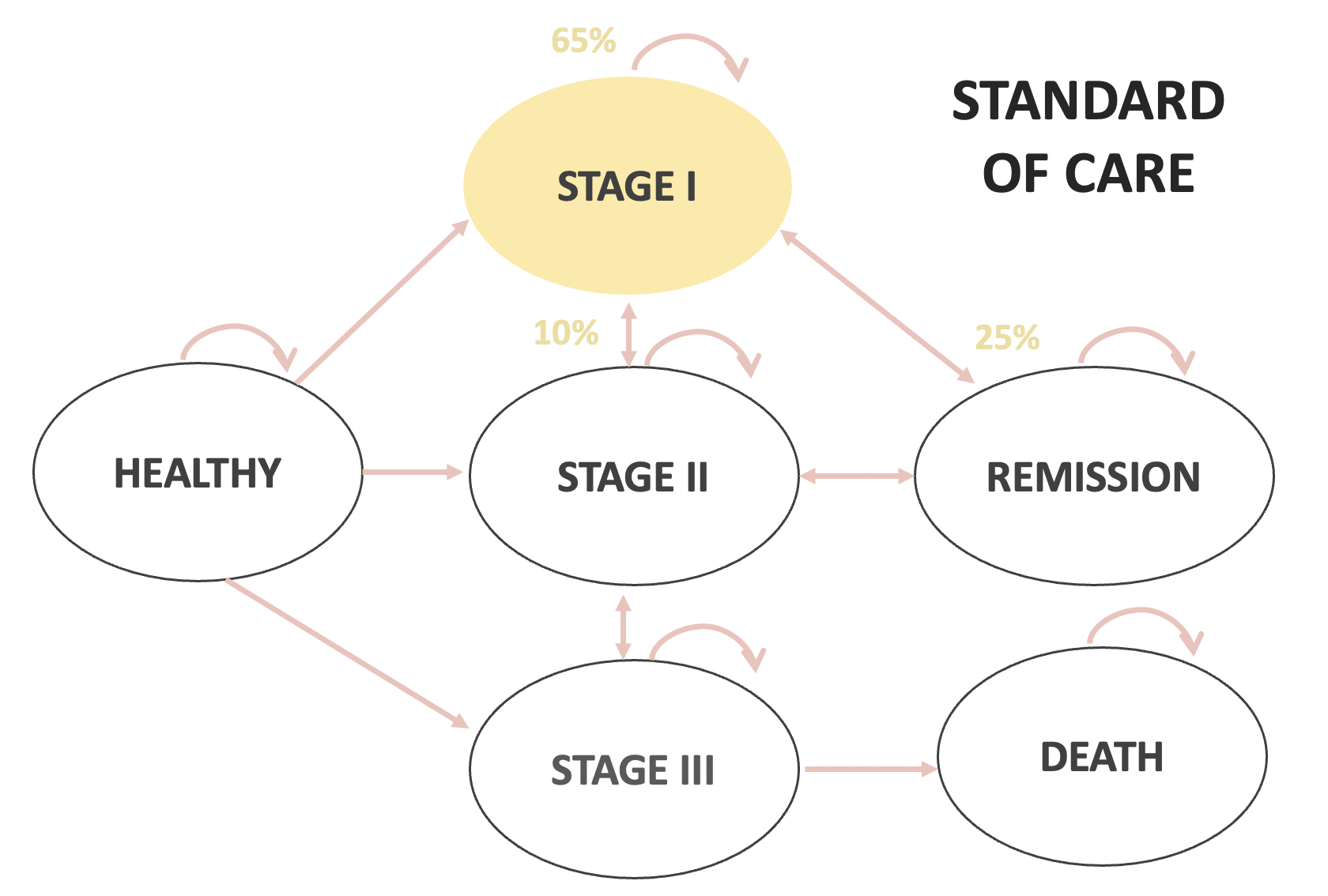
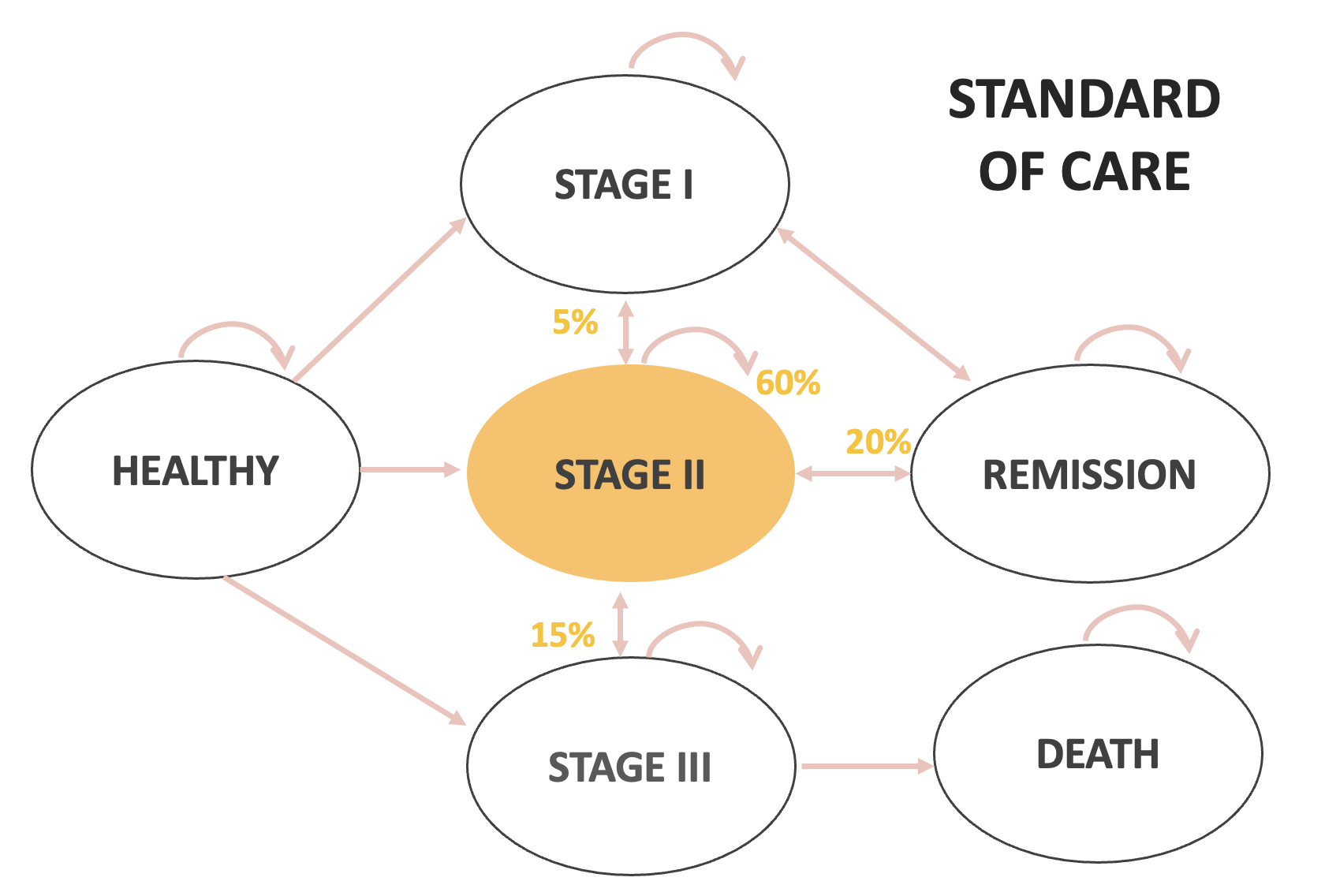
In-class example

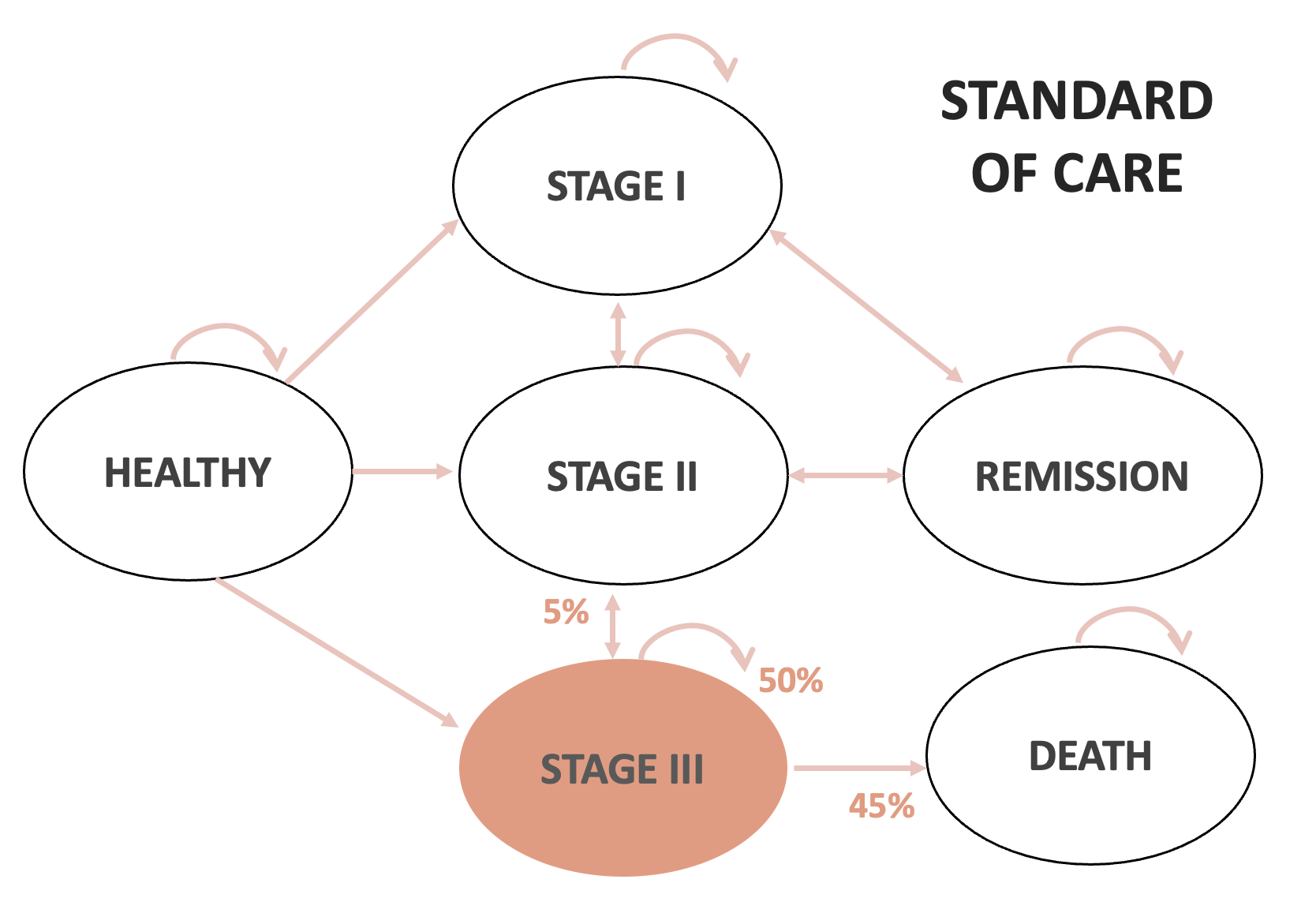
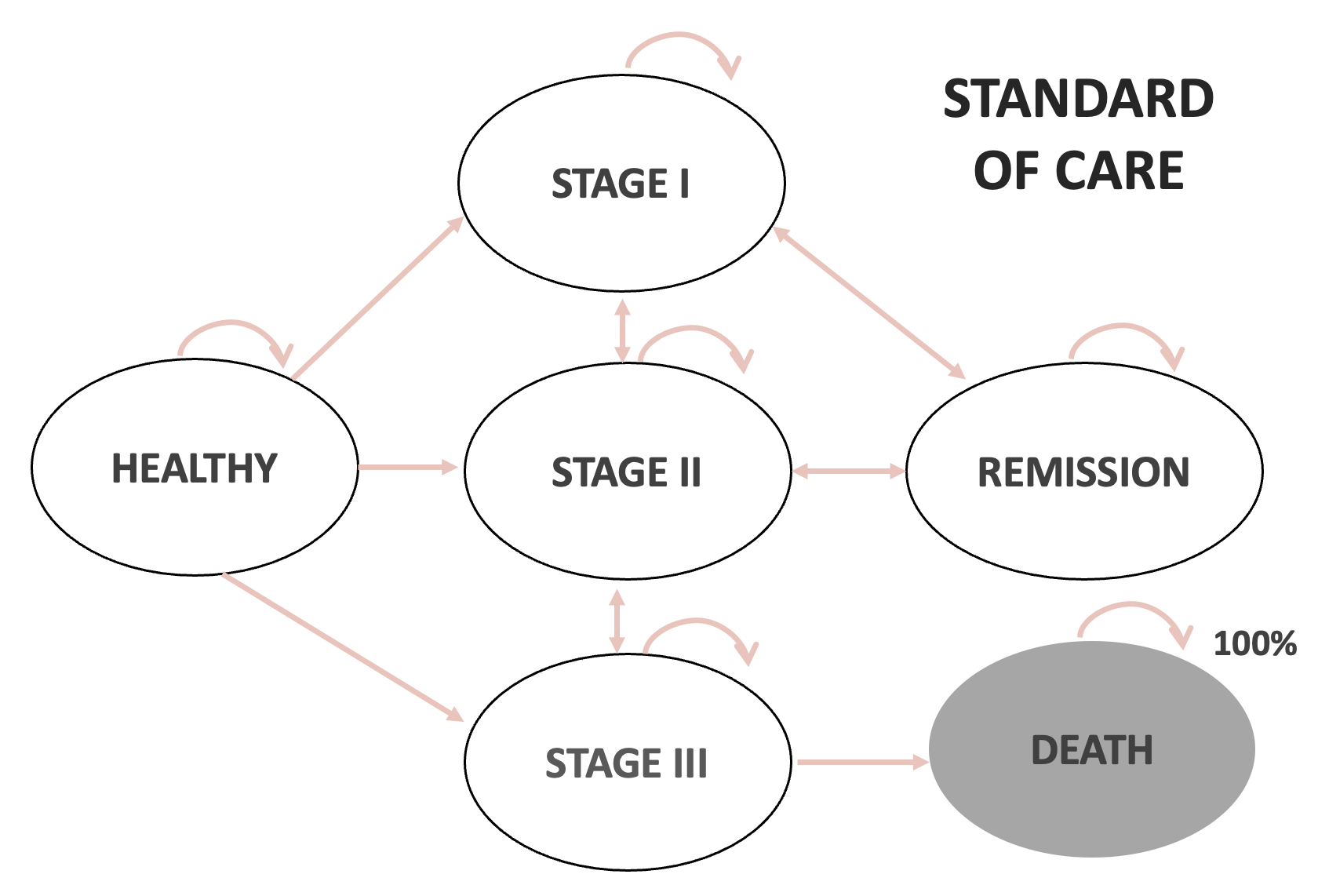
In-class example

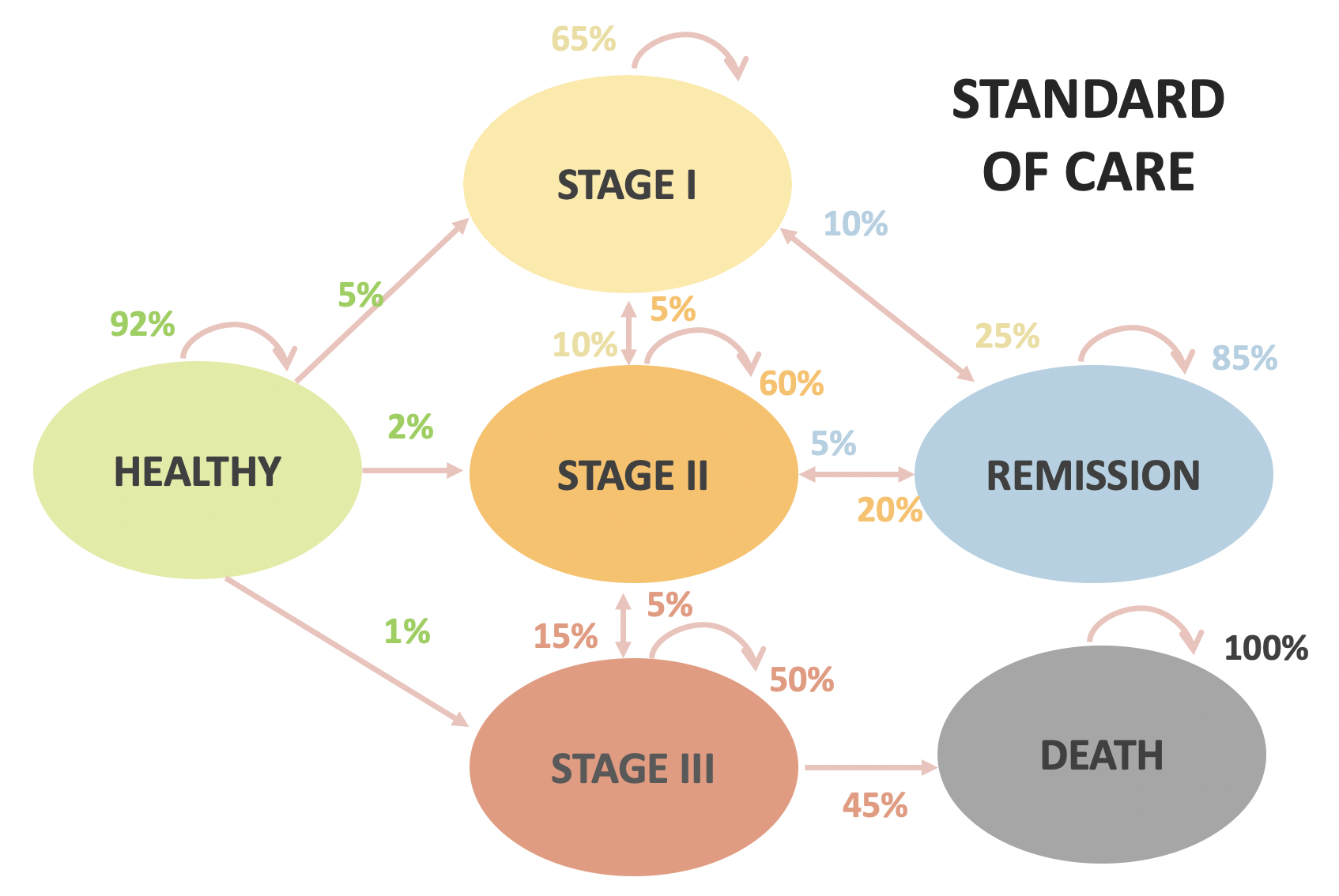
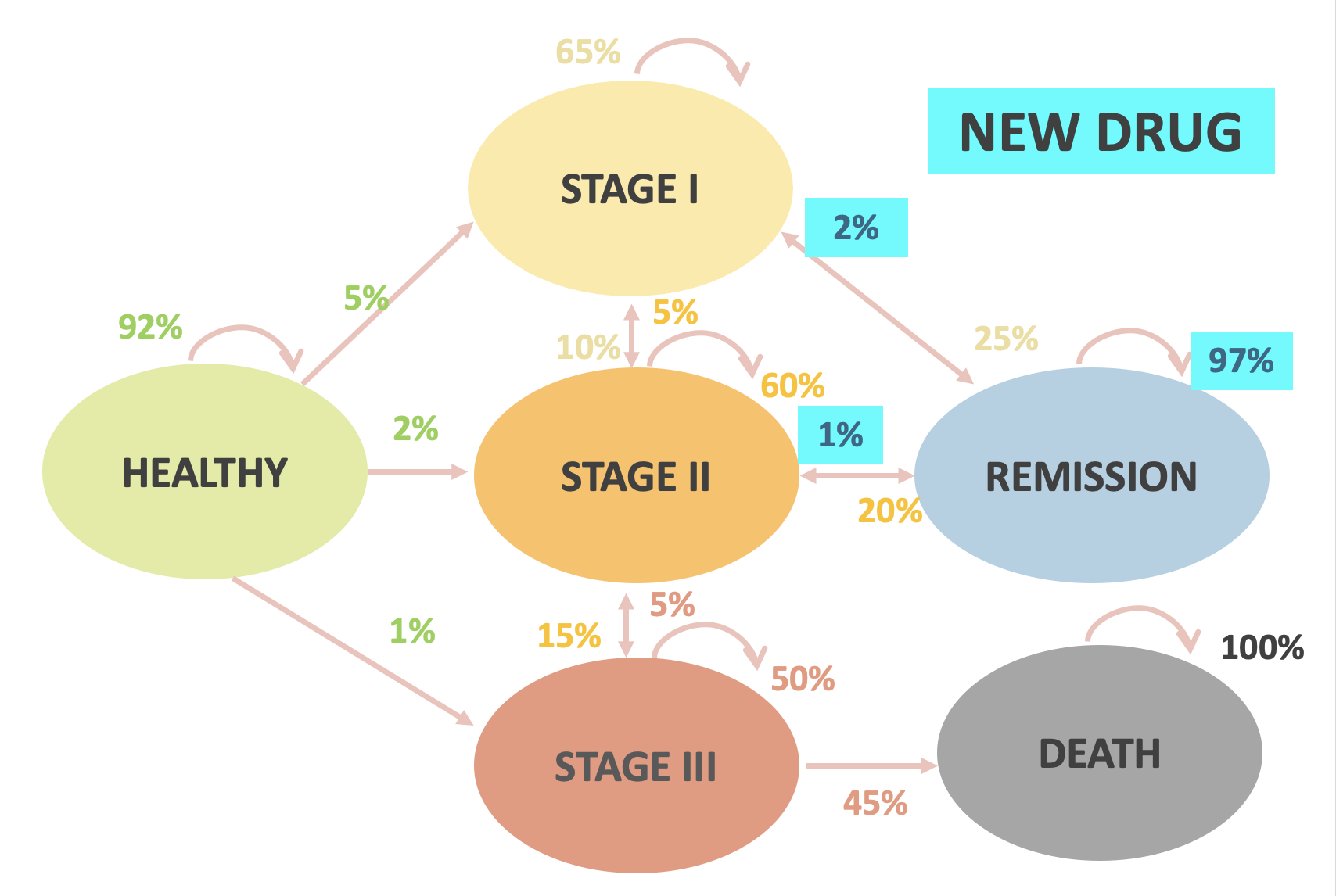
In-class example

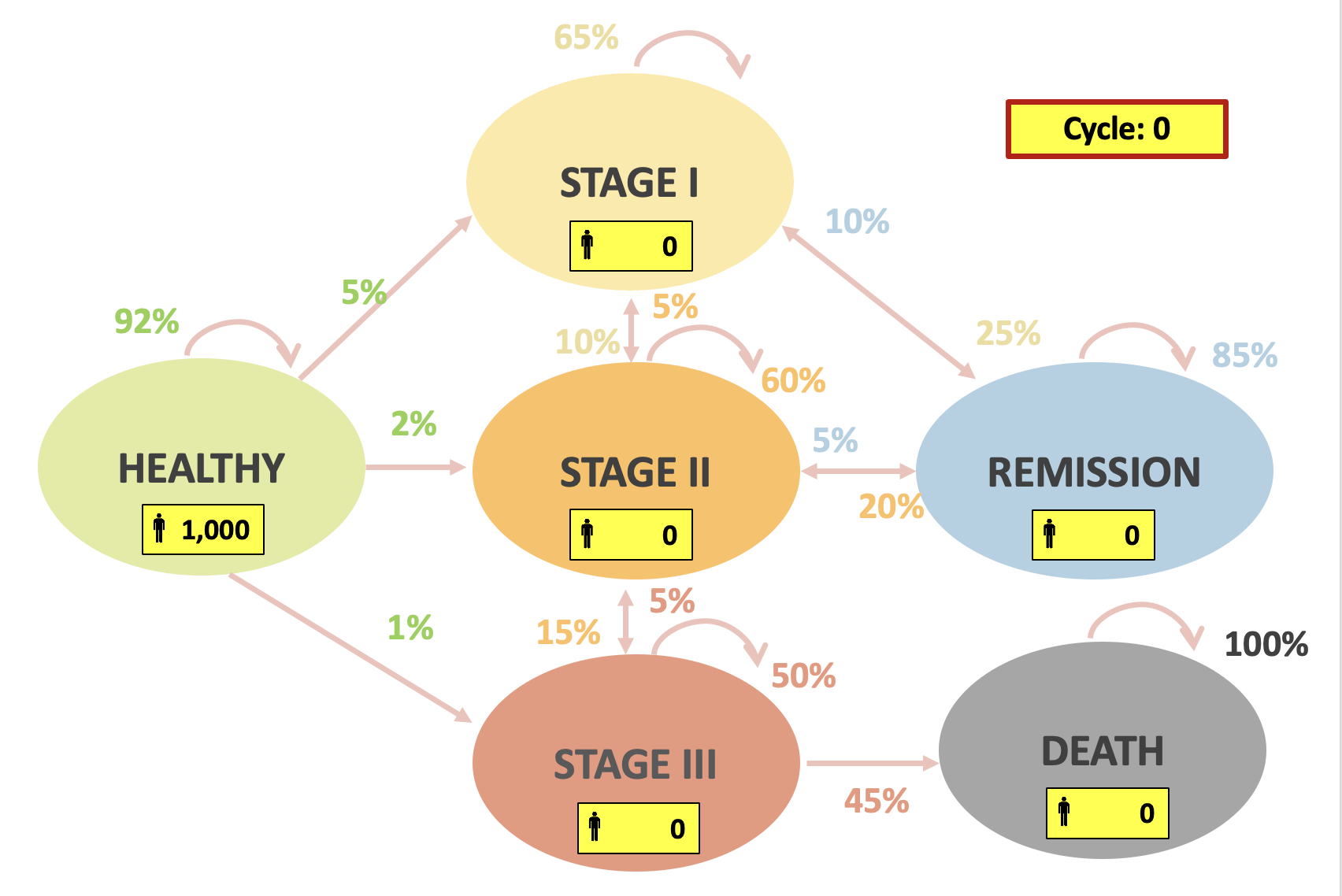
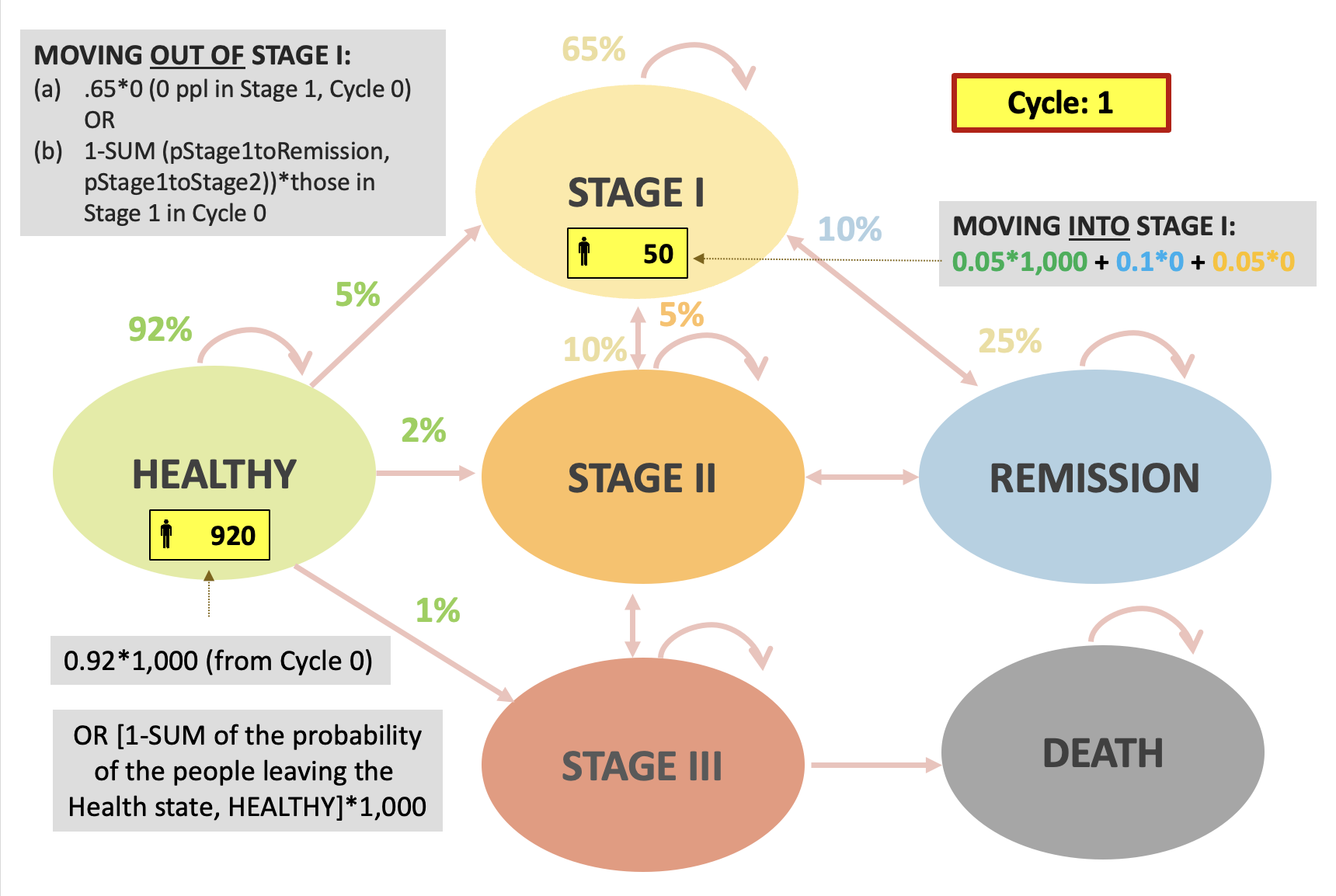
In-class example

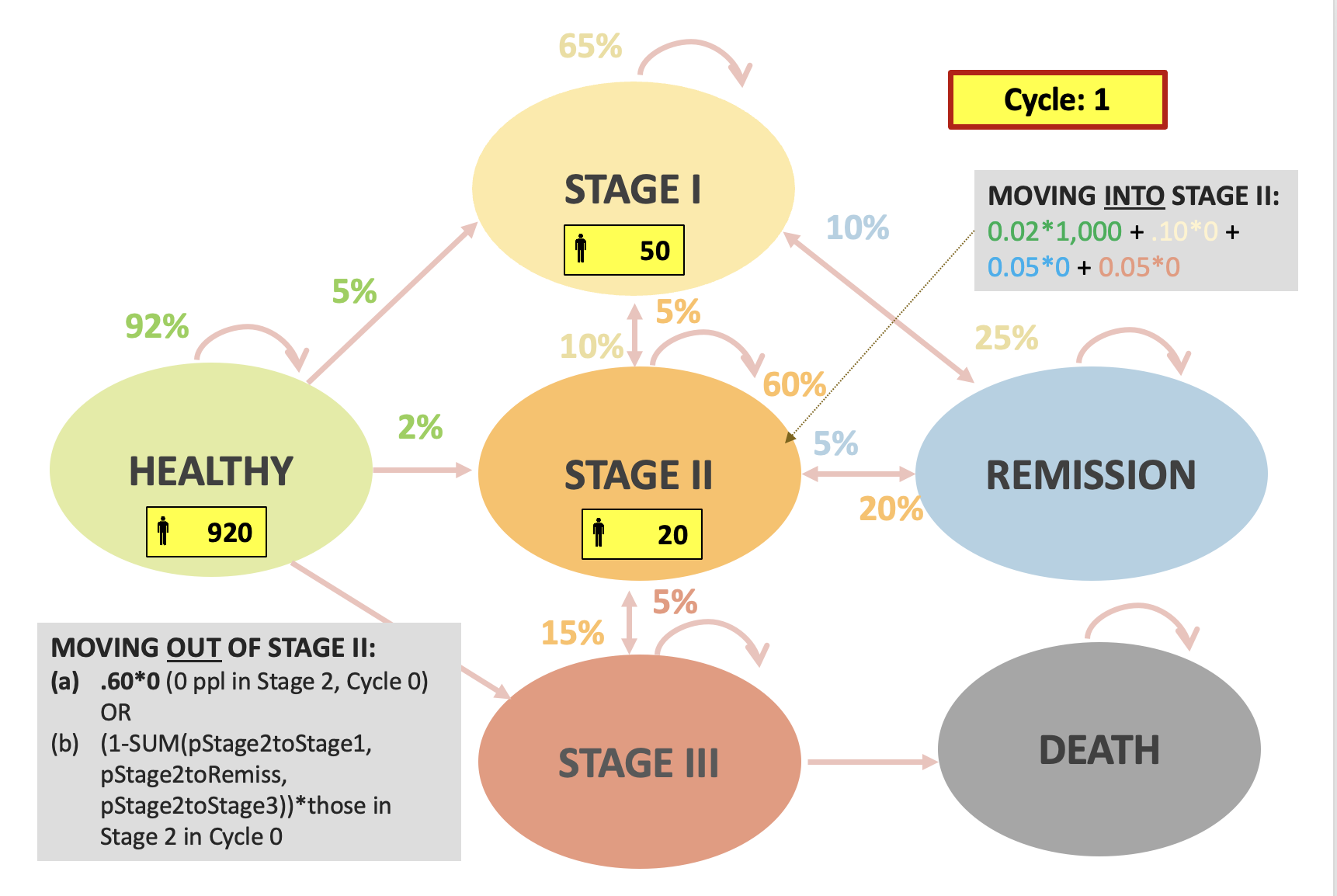
Calculating Outcomes

An example Markov Trace (75 year horizon)

Cycle	Healthy	Sick	Dead
0	1.000	0.000	0.000
1	0.856	0.138	0.007
2	0.732	0.253	0.015
3	0.626	0.349	0.025
4	0.536	0.429	0.035
5	0.458	0.495	0.046
…	…	…	…
75 (End)	0	0.282	0.718

Markov Traces

• Often we are modeling several competing strategies.
• Each strategy has its own transition probability matrix.
• Therefore, each strategy will have it’s own Markov trace.

Calculating Outcomes

• With our markov traces complete, we can calculate expected outcomes (e.g., costs, QALYs, DALYs, etc.).
• Much like we did with decision trees, we need to define “payoffs” for each health state.

Defining Payoffs

• Cost outcomes: Cost of being healthy, sick, dead (including any additional costs of treatment/intervention, if applicable).
• QALY outcomes: Utility weight of being healthy (usually 1.0), sick, dead (usually 0.0).
• DALY outcomes: Disability weights of being sick (YLD) and remaining life expectancy based on reference life table (YLL)

Defining Payoffs

• We can calculate the total payoff for each cycle by multiplying the number or fraction of the cohort in each health state by its payoff value, and adding them together.

Example Markov Trace (two cycles):

Cycle	Healthy	Sick	Dead
0	1.000	0.000	0.000
1	0.856	0.138	0.007

Example: Life Years

• We’ll build our example using a simple outcome: expected life years under a given strategy.
• Payoffs:
  • Healthy: 1.0
  • Sick: 1.0 [they’re still alive!]
  • Dead: 0.0

Example: Life Years

• To get the total “payoff” for a given cycle, we multiply the fraction of the cohort in a given health state by the payoff associated with that health state.
• Do this for each health state, and add them together to get the total.

Cycle	Healthy	Sick	Dead	LY
0	1.000	0.000	0.000
1	0.856	0.138	0.007

Example: Life Years

What is the LY “payoff” for Cycle 0?

Cycle	Healthy	Sick	Dead	LY
0	1.000	0.000	0.000
1	0.856	0.138	0.007

Example: Life Years

What is the LY “payoff” for Cycle 0?

Cycle	Healthy	Sick	Dead	LY
0	1.000	0.000	0.000	1.0 = 1.0 * 1.0 + 0.0 * 1.0 + 0.0 * 0.0
1	0.856	0.138	0.007

Example: Life Years

What is the LY “payoff” for Cycle 1?

Cycle	Healthy	Sick	Dead	LY
0	1.000	0.000	0.000	1.0
1	0.856	0.138	0.007	0.994 = 0.856 * 1.0 + 0.138 * 1.0 + 0.007 * 0.0

… and so on.

Example: Life Years

Cycle	Healthy	Sick	Dead	LY
0	1.000	0.000	0.000	1
1	0.856	0.138	0.007	0.993
2	0.732	0.253	0.015	0.985
3	0.626	0.349	0.025	0.975
4	0.536	0.429	0.035	0.965
5	0.458	0.495	0.046	0.954
…	…	…	…
75 (End)	0	0.282	0.718	0.282

Example: Costs

• Now suppose we want to calculate costs.
• Payoffs:
  • Healthy: $0
  • Sick: $1,000
  • Dead: $0

Example: Costs

What is the Cost “payoff” for Cycle 0?

Cycle	Healthy	Sick	Dead	Cost
0	1.000	0.000	0.000
1	0.856	0.138	0.007

Example: Costs

What is the Cost “payoff” for Cycle 0?

Cycle	Healthy	Sick	Dead	Cost
0	1.000	0.000	0.000	0 = 1.00 * 0 + 0.0 * 1000 + 0.0 * 0
1	0.856	0.138	0.007

Example: Costs

What is the cost “payoff” for Cycle 1?

Cycle	Healthy	Sick	Dead	Cost
0	1.000	0.000	0.000	0
1	0.856	0.138	0.007	138 = 0.856*0+0.138*1000+0.007*0

… and so on.

Other Outcomes

• We can repeat a similar process for health outcomes (e.g., QALYs, YLDs) by multiplying the “payoff” (e.g., utility weight, disability weight) for a given health state by the fraction of the cohort in that health state in the cycle.

Calculating Total Expected Outcomes

Total Outcomes

Total Life Years

Let’s look at the Markov trace and cycle outcomes for the Life Year outcome.

Cycle	Healthy	Sick	Dead	LY (single cycle)
0	1.000	0.000	0.000	1
1	0.856	0.138	0.007	0.993
2	0.732	0.253	0.015	0.985
3	0.626	0.349	0.025	0.975
4	0.536	0.429	0.035	0.965
5	0.458	0.495	0.046	0.954
…	…	…	…
75 (End)	0	0.282	0.718	0.282

Life years

We can create a new column that accumulates life years over each cycle.

Cycle	Healthy	Sick	Dead	LY (single cycle)	LY (cumulative)
0	1.000	0.000	0.000	1	1
1	0.856	0.138	0.007	0.993	1 + 0.993 = 1.993
2	0.732	0.253	0.015	0.985
3	0.626	0.349	0.025	0.975
4	0.536	0.429	0.035	0.965
5	0.458	0.495	0.046	0.954
…	…	…	…	…
75 (End)	0	0.282	0.718	0.282

Life years

Cycle	Healthy	Sick	Dead	LY (single cycle)	LY (cumulative)
0	1.000	0.000	0.000	1	1
1	0.856	0.138	0.007	0.993	1.993
2	0.732	0.253	0.015	0.985	1 + 0.993 + 0.985 = 2.978
3	0.626	0.349	0.025	0.975
4	0.536	0.429	0.035	0.965
5	0.458	0.495	0.046	0.954
…	…	…	…	…
75 (End)	0	0.282	0.718	0.282

Life years

• The cumulative LYs for an individual starting in the Healthy state is 44.825

• Note that this is within a 75 years time horizon

Cycle	Healthy	Sick	Dead	LY (single cycle)	LY (cumulative)
0	1.000	0.000	0.000	1	1
1	0.856	0.138	0.007	0.993	1.993
2	0.732	0.253	0.015	0.985	2.978
3	0.626	0.349	0.025	0.975	3.954
4	0.536	0.429	0.035	0.965	4.919
5	0.458	0.495	0.046	0.954	5.872
…	…	…	…	…	…
75 (End)	0	0.282	0.718	0.282	44.825

Total Outcomes

• We can do a similar exercise to get total costs, total QALYs, total DALYs, etc.
• However, it’s not that simple. There are some extra complications we have to deal with.
  • Discounting
  • Cycle correction

Cycle correction

The problem

• In real life, events could occur at any points in a given cycle, but a Markov model assumes all events occur either at the beginning or end of each cycle

• Time is continuous, so are survival/event-free survival curves

• When we discretize time by using a fixed cycle length, we can make two assumptions

  • Suppose this is a simple Well \rightarrow Dead process

The problem

Assuming death happens at the end of cycle (A)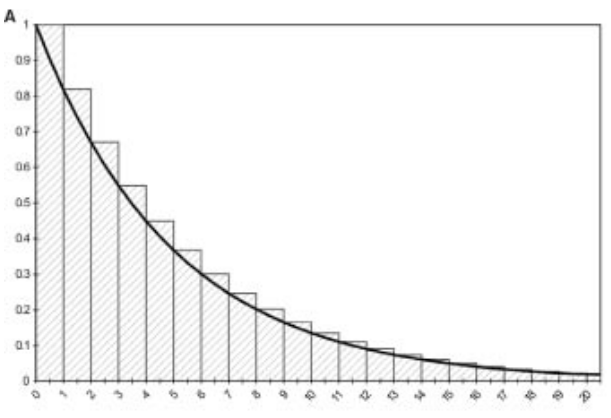

Overestimates state membership in Well

Assuming death happens at the start of cycle (B)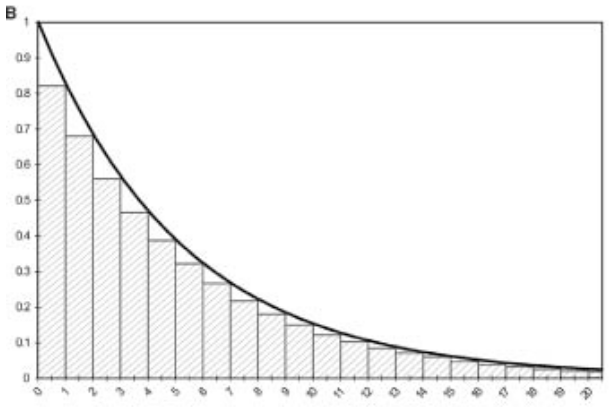

Underestimates state membership in Well

Source

The problem

1. When counting subjects at the END of cycle (top visual) (transition happens at beginning of cycle) - you would be underestimating LYs

• Say you have 10 people & 5 die halfway through, you wouldn’t be counting the 5 that started that has accumulated SOME costs & benefits in that cycle; you would only be counting the “end” survivors.

2. If you counted subjects at BEGINNING of cycle (the bottom visual) (transition happens at end of previous cycle), you would be overestimating LYs

• For example, for these 10 people, they die halfway through the cycle, but you already gave that person the full cycle’s benefits & costs at the beginning (even though they shouldn’t get the full benefits & costs because they died halfway through)

Half-cycle correction

Source

Half-cycle correction

Source

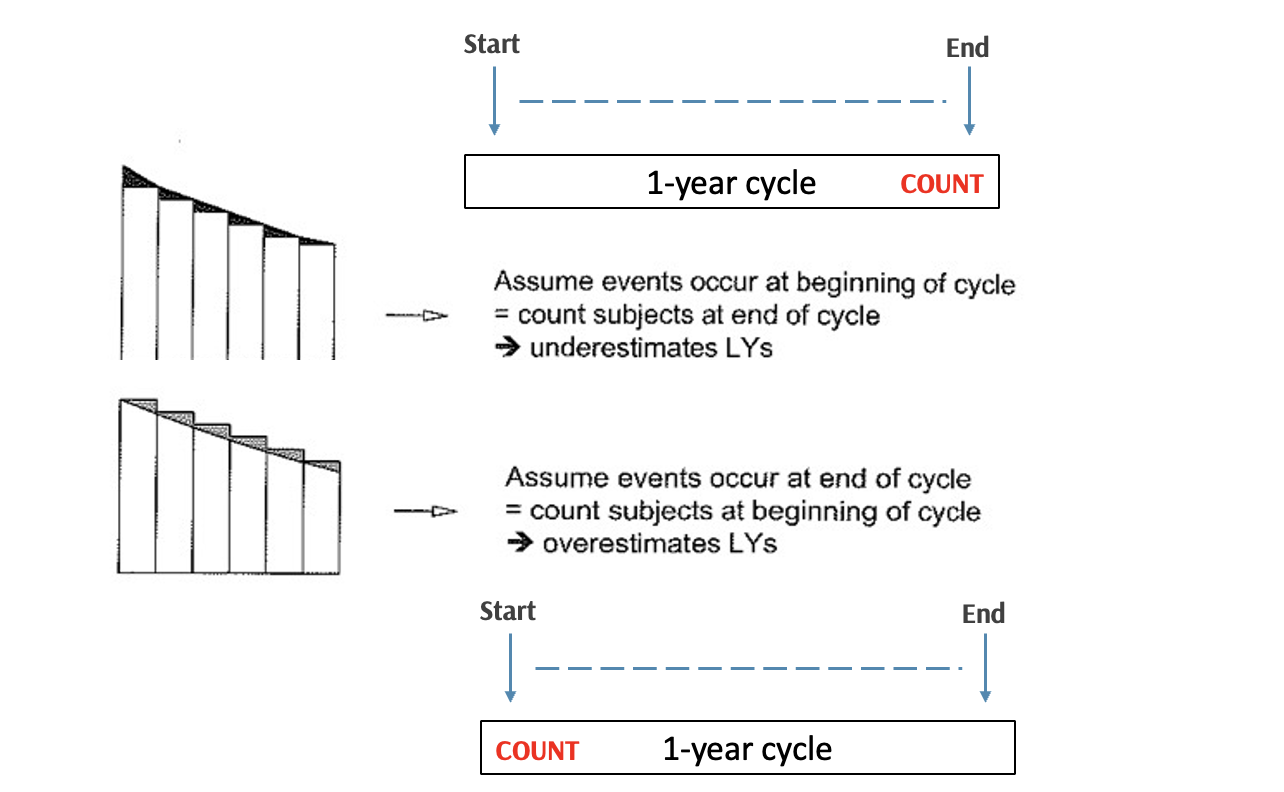
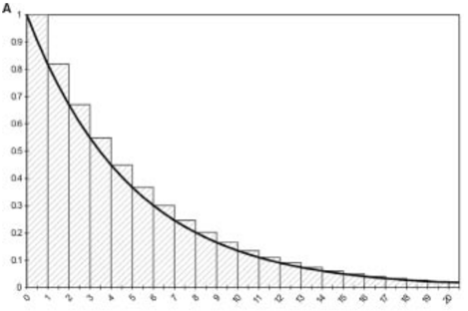
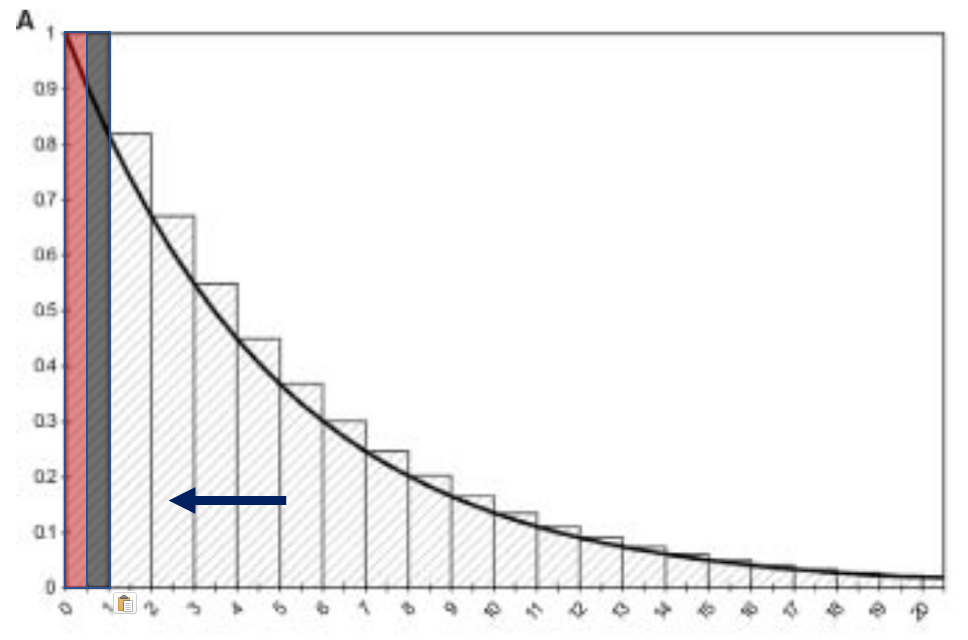
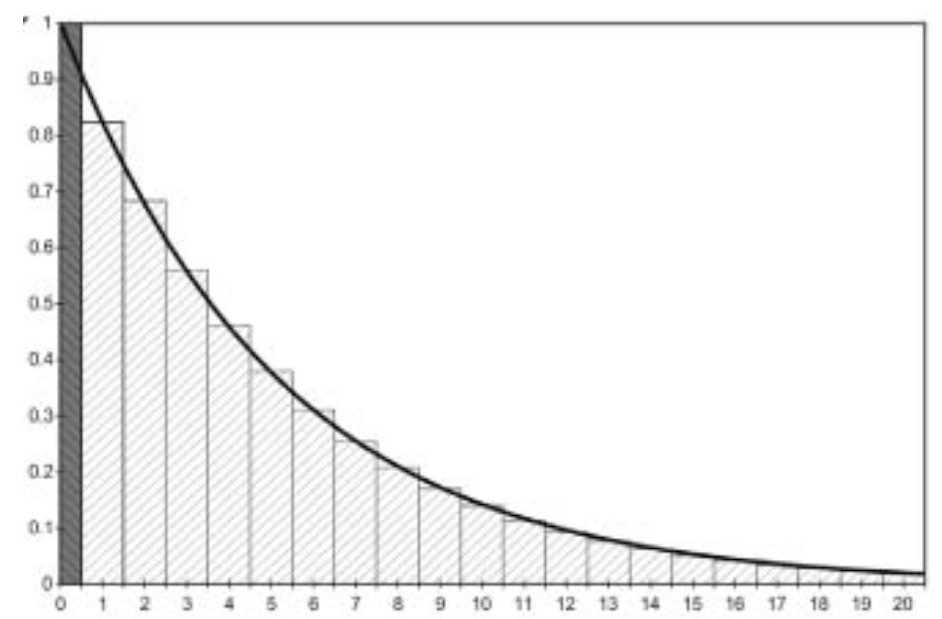
Half-cycle correction

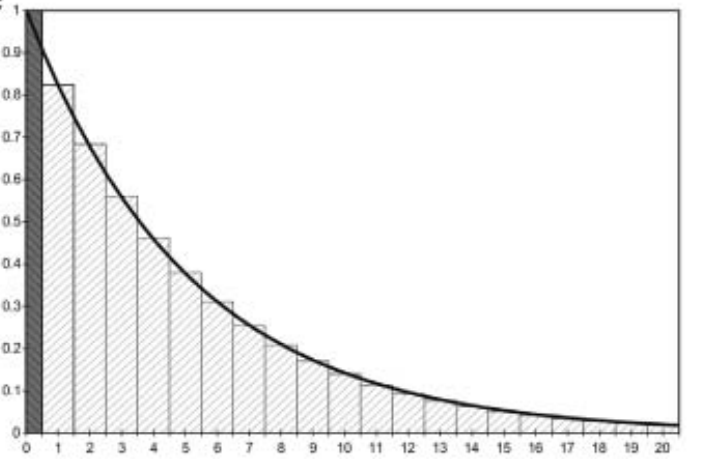
• Multiply the outcomes by 1/2 in the first and last cycle.

• Shifting the computed, discrete state membership curve to the left by 1/2 cycle.

• Essentially assuming that events happen in the middle of cycle

Source

Half-cycle correction

1. Intuition behind it – the image to the left represents underestimation

2. & you can see if you line that up to the Y-AXIS (center figures), the triangular areas can be seen to be equal to a rectangle one-half cycle wide extending from 0 to 1.

3. If you add back the original rectangles, the approximation is NOW BETTER – it has corrected for the underestimation.

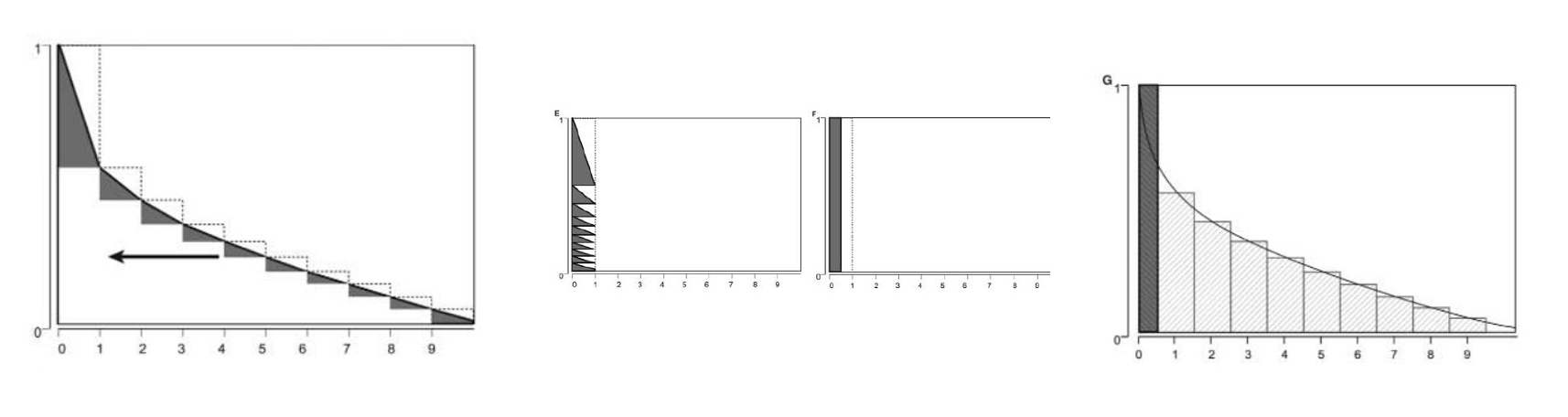
Apply cycle correction methods to our markov trace…

Half-cycle correction

• Multiply the outcomes by 1/2 in the first and last cycle.

Cycle	Healthy	Sick	Dead	LY (single cycle, adjusted)	LY (cumulative)
0	1.000	0.000	0.000	1*0.5	0.5
1	0.856	0.138	0.007	0.993	0.5 + 0.993 = 1.493
2	0.732	0.253	0.015	0.985	2.478
3	0.626	0.349	0.025	0.975	3.454
4	0.536	0.429	0.035	0.965	4.419
5	0.458	0.495	0.046	0.954	5.372
…	…	…	…	…	…
75 (End)	0	0.282	0.718	0.282 *0.5	44.184

This number is smaller than our original estimate without half-cycle correction (44.825!)

Summary

• Once we have total (discounted, half-cycle corrected) outcomes for each strategy, we can turn to conducting incremental cost-effectiveness analysis.
• We covered these methods yesterday!

Markov Models

Pros	Cons
Can model repeated events	Can only transition once in a given cycle
Can model more complex + longitudinal clinical events	Shortening the cycle can create computational challenges.
Not computationally intensive; efficient to model and debug	Shortening cycle can cause “state explosion” if tunnel states are used

Next up: Markov Case Study