Review of Day 1 Concepts
Decision Trees
Strengths
- They are easy to describe and understand
- Works well with limited time horizon
- Decision trees are a powerful framework for analyzing decisions and can provide rapid/useful insights, but they have limitations.
Limitations
- No explicit accounting for the elapse of time.
- Recurrent events must be separately built into model.
- Fine for short time cycles (e.g., 12 months) but we often want to model over a lifetime.
- Difficult to incorporate real clinical detail - Tree structure can quickly become complex.
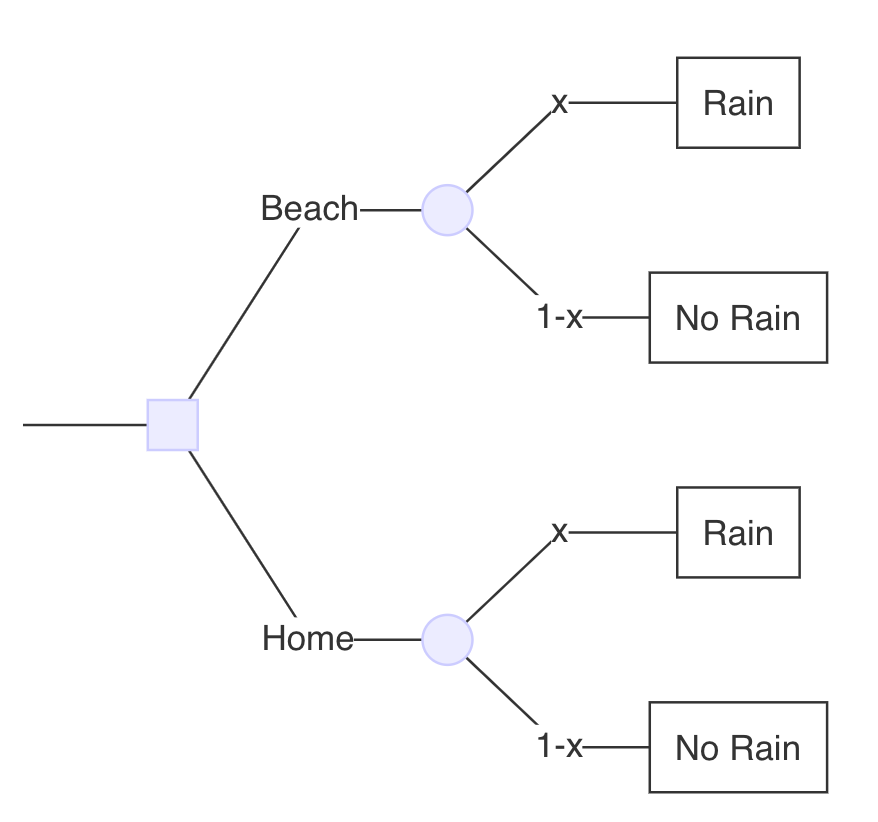
At what probability (p_B) of rain for the beach are you indifferent between the two options?
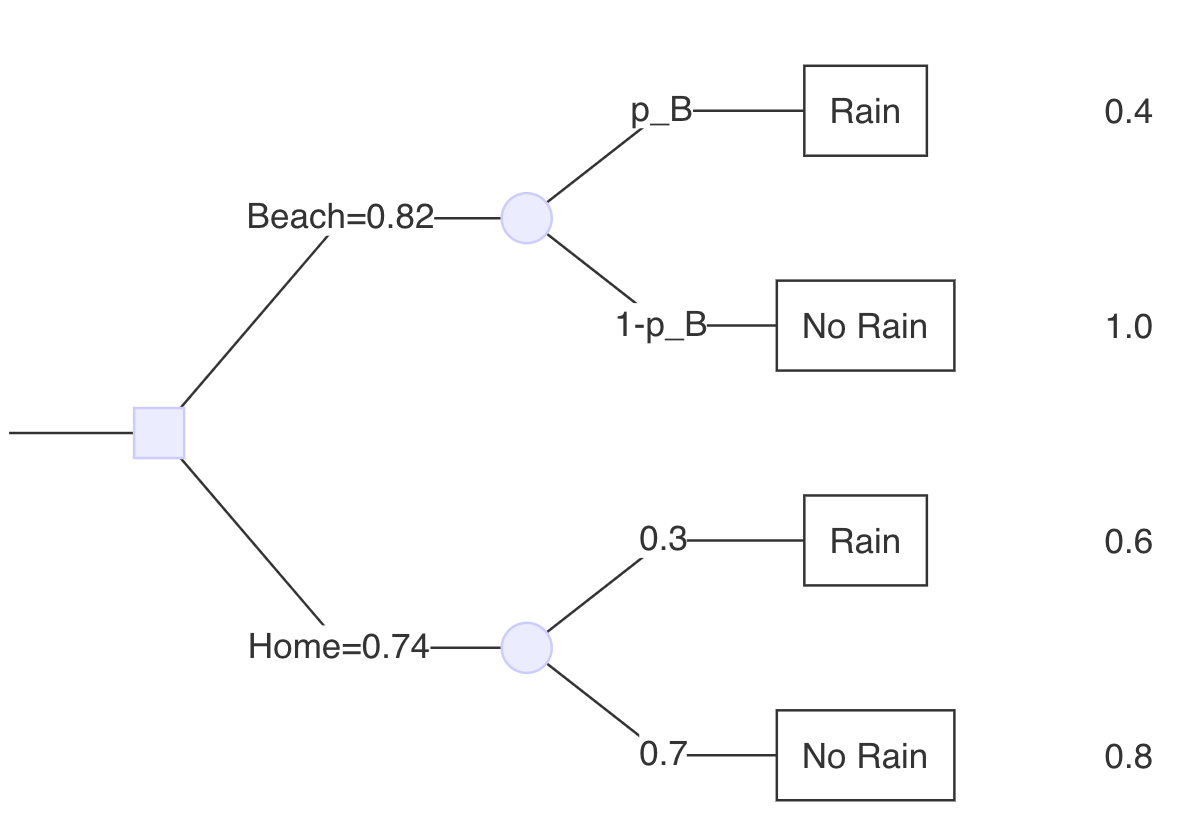
At what probability (p_B) of rain for the beach are you indifferent between the two options?
Earlier, we solved for the expected payoff of remaining at home: 0.74 (which was a lower expected value than going to the beach when the chance of rain at both was 30%)
What would p_B need to be to yield an expected payoff at the beach of 0.74?
- In other words, at what probability of rain at the beach would you be indifferent between staying at home & going to the beach?
At what probability (p_B) of rain for the beach are you indifferent between the two options?
Set 0.74 (expected value of remaining at home) equal to the beach payoffs and solve for p_B
pB * 0.4 + (1 - pB) * 1.0 = 0.74
At what probability (p_B) of rain for the beach are you indifferent between the two options?
pB * 0.4 + (1 - pB) * 1.0 = 0.74
pB * 0.4 + 1 - pB = 0.74
At what probability (p_B) of rain for the beach are you indifferent between the two options?
pB * 0.4 + 1 - pB = 0.74
pB * -0.6 = -0.26
At what probability (p_B) of rain for the beach are you indifferent between the two options?
pB * -0.6 = -0.26
pB = -0.26 / -0.6 = 0.43
At what probability (p_B) of rain for the beach are you indifferent between the two options?
When the probability of rain at the beach is 43% (probability of rain at home remains at 30%), we would be indifferent between staying at home & going to the beach.
If the probability of rain at the beach in > 43%, then we would stay home
Threshold Example: Screening Program
Decision Tree: Pulmonary Embolism
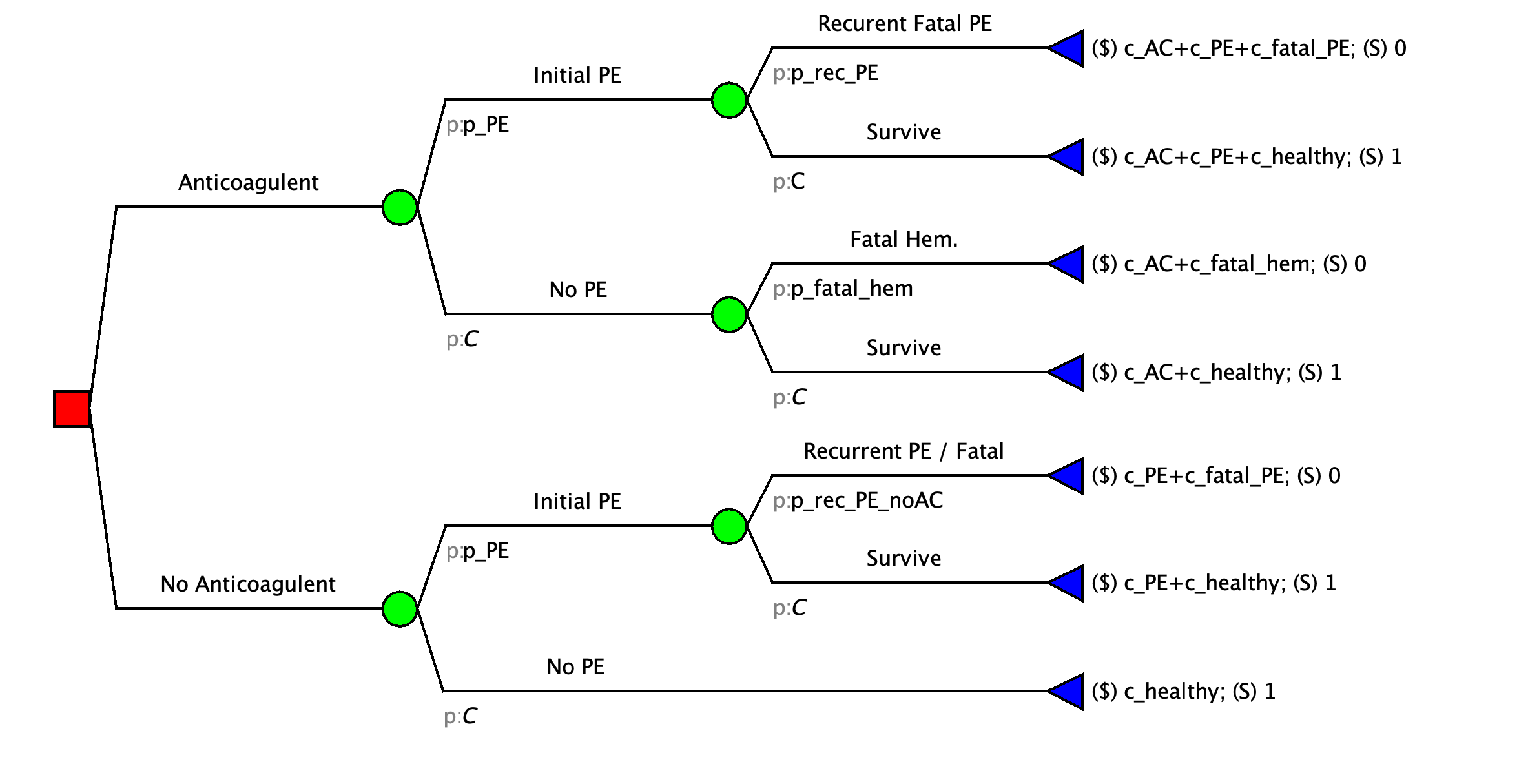
Decision Tree: Pulmonary Embolism
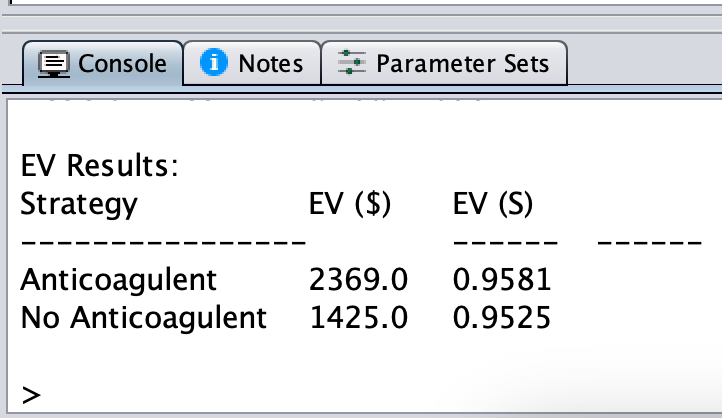
Parameter Uncertainty
Suppose we are not certain about the probability of fatal hemorrhage.
At what value of
p_fatal_hemwould expected survival be equal?
Threshold Analysis: Idea
Allow the value of
p_fatal_hemto vary over a range.Find the value of
p_fatal_hemalong this range where expected survival is equal for the “Anticoagulant” and “No Anticoagulant” strategies.
Threshold Analysis
Threshold Analysis
Threshold Analysis

Threshold Analysis
Threshold Analysis

Example 2: Screening Program
Screening Program
- The Ministry of Health is considering implementation of a population-wide treatment program for a costly disease that affects a subgroup of the population.
- The prevalence of the disease is not well-established.
Screening Program
- An inexpensive screening test is available, but it is not perfect at detecting individuals with the disease.
- A more expensive (perfect) diagnostic test is available.
Decision Problem
- Do nothing.
- Population screening with the inexpensive test.
- Expensive diagnostic test for everyone.
Decision Problem
- Given that we do not know the underlying probability of disease (
p_disease), can we make a policy decision? - Perhaps! We can use a threshold analysis.
Threshold Analysis: Steps
- Allow
p_diseaseto vary over a plausible range. - Find the threshold at which we would be indifferent between:
- Do nothing vs. population screening with inexpensive test.
- Population screening vs. diagnostic test for everyone.
Threshold Analysis
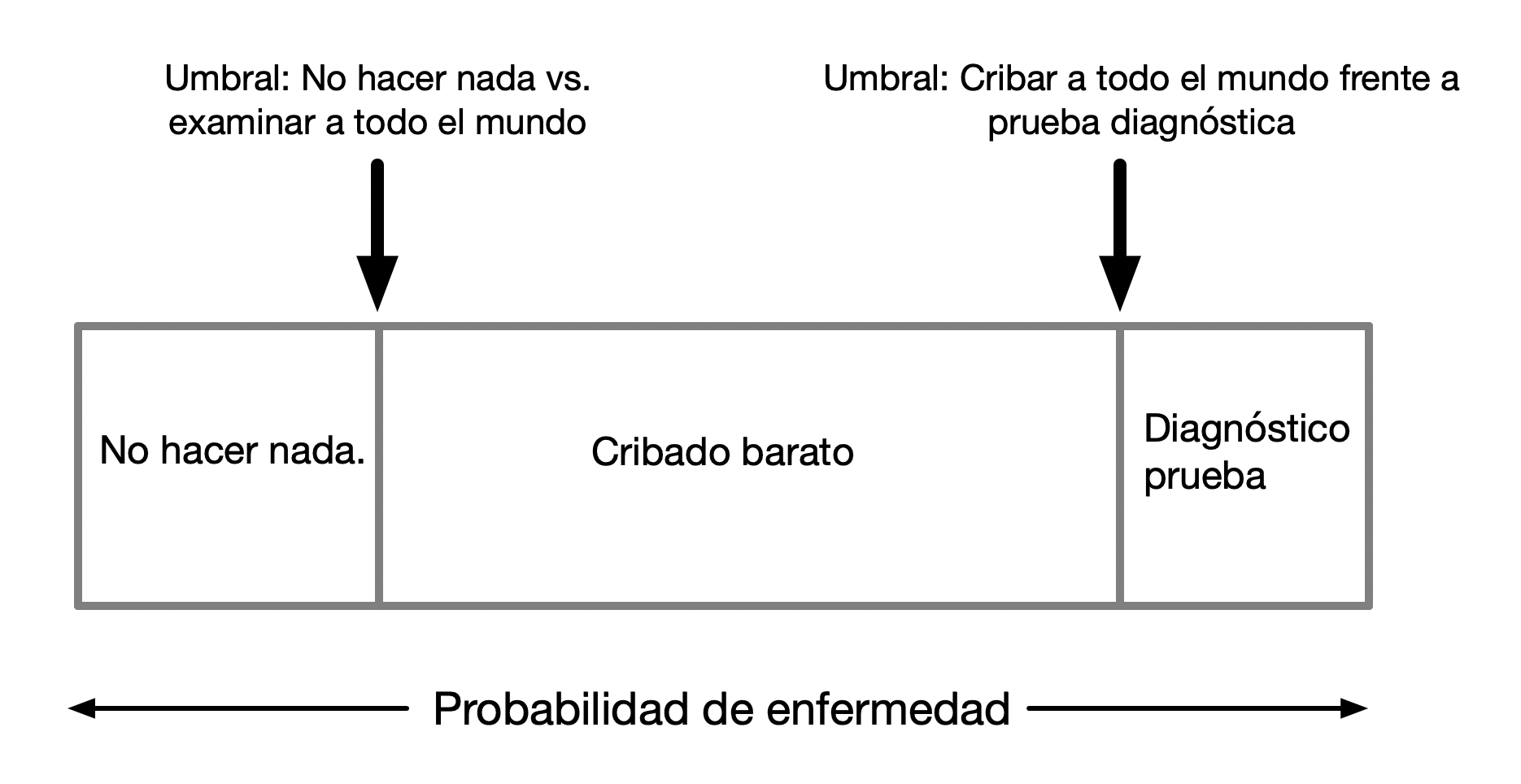
Decision
- We can now solicit expert opinion on a likely range of the disease prevalance.
- If this range falls within the thresholds, we can make a decision despite uncertainty in the underlying disease prevalence.
