Repaso de los conceptos del primer día

Árboles de decisión

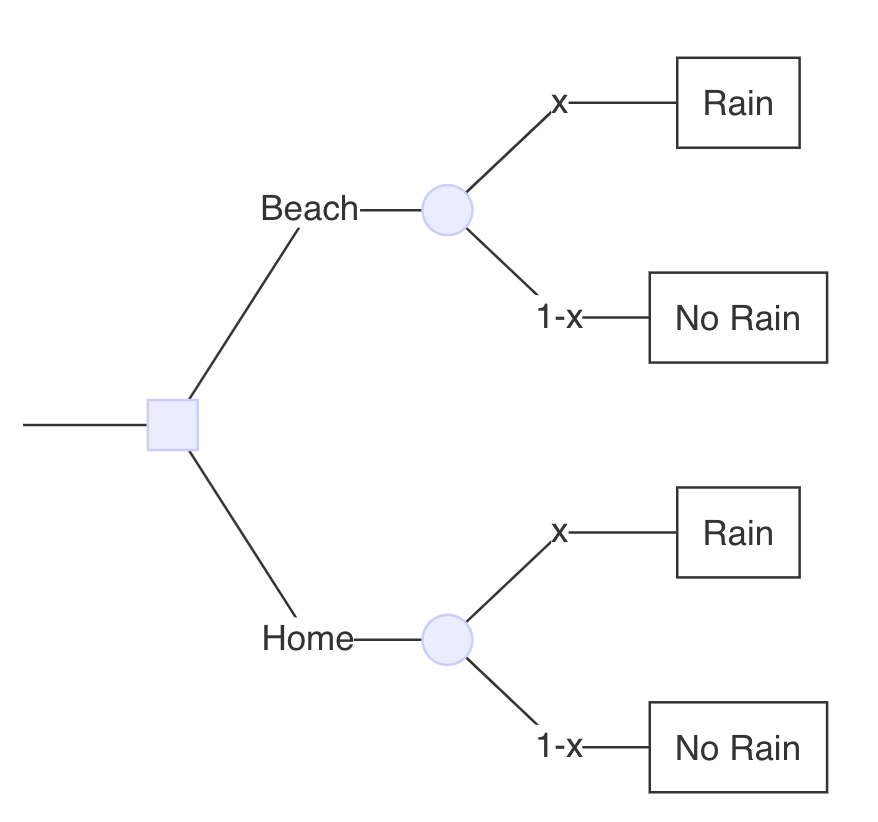
Ventajas

• Son fáciles de describir y entender
• Funcionan bien con un horizonte temporal limitado
• Los árboles de decisión son un marco potente para analizar decisiones y pueden proporcionar perspectivas rápidas/útiles, pero tienen limitaciones.

Limitaciones

• No toman en cuenta explícitamente el paso del tiempo.
  • Los sucesos recurrentes deben incorporarse por separado al modelo.
  • Está bien para ciclos de tiempo cortos (por ejemplo, 12 meses), pero a menudo queremos modelizar a lo largo de toda la vida.
• Es difícil incorporar detalles clínicos reales. La estructura de árbol puede volverse compleja rápidamente.

¿A qué probabilidad (p_B) de lluvia para la playa estaríamos indiferente entre las dos opciones?

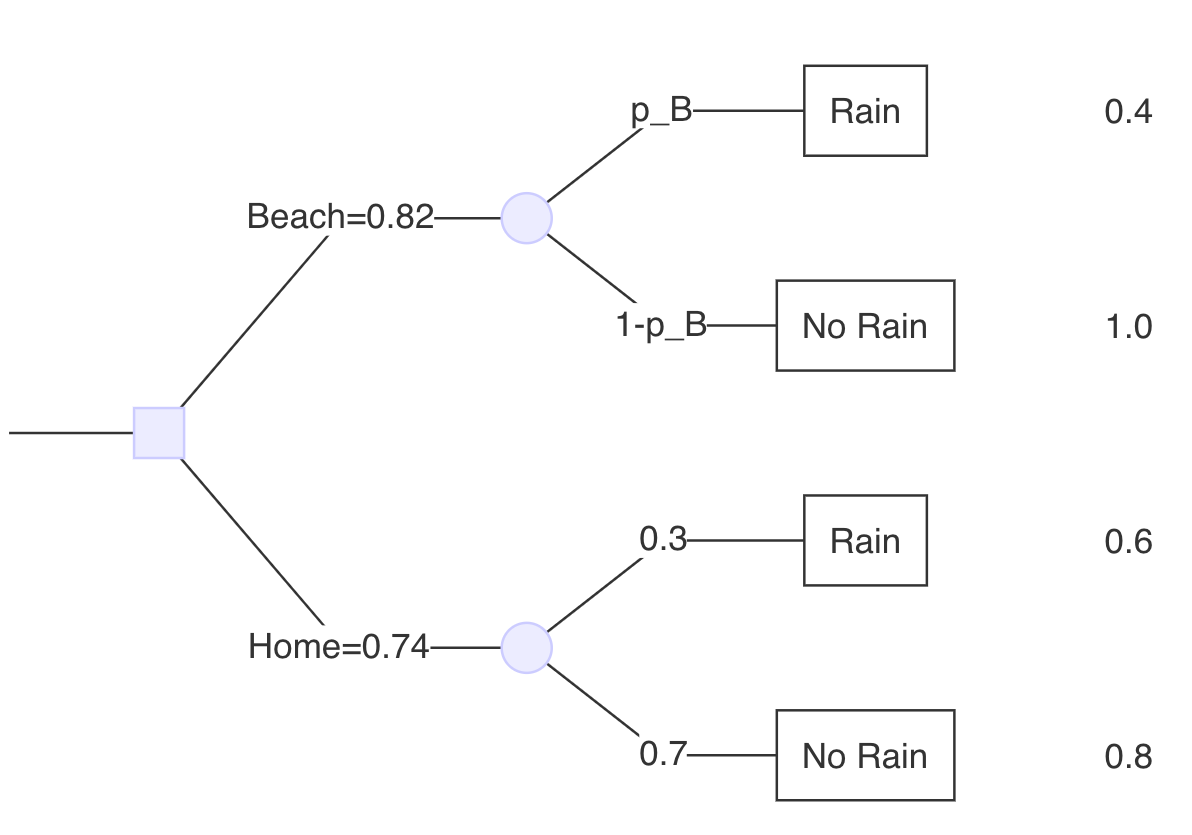
¿A qué probabilidad (p_B) de lluvia para la playa estaríamos indiferente entre las dos opciones?

• Antes hemos calculado el beneficio esperado de quedarse en casa: 0,74 (que era un valor esperado menor que ir a la playa cuando la probabilidad de lluvia en ambos era del 30%)
  

• ¿Cuál tendría que ser** p_B para obtener una recompensa esperada en la playa playa de 0,74?

  • En otras palabras, ¿con qué probabilidad de lluvia en la playa ¿le resultaría indiferente quedarse en casa o ir a la playa?

1. Formulemos ahora una pregunta ligeramente distinta. probabilidad….
2. Supongamos ahora que la probabilidad de lluvia para la opción CASA no cambia (por lo que se mantiene en 0,3)
3. DIFERENCIA CLAVE CON RESPECTO AL ÚLTIMO EJEMPLO: En el último ejemplo, las probabilidades eran las mismas y queríamos obtener nuestro umbral de indiferencia entre la playa y quedarse en casa
4. **Ahora estamos suponiendo que todavía hay una probabilidad del 30% de que que llueva si te quedas en casa, pero ¿a qué probabilidad de lluvia en la playa te sería indiferente entre las dos opciones? (Puesto que elegimos la playa cuando ambas probabilidades eran iguales al 30%)

• En otras palabras, ¿con qué probabilidad de LLOVER EN LA PLAYA sería indiferente entre la playa y su casa

¿A qué probabilidad (p_B) de lluvia para la playa estaríamos indiferente entre las dos opciones?

Fije 0,74 (valor esperado de quedarse en casa) igual a la playa y resuelva para p_B.

p_B * 0.4 + (1 - p_B) * 1.0 = 0.74

¿A qué probabilidad (p_B) de lluvia para la playa estaríamos indiferente entre las dos opciones?

p_B * 0.4 + (1 - p_B) * 1.0 = 0.74

p_B * 0.4 + 1 - p_B = 0.74

¿A qué probabilidad (p_B) de lluvia para la playa estaríamos indiferente entre las dos opciones?

p_B * 0.4 + 1 - p_B = 0.74

p_B * -0.6 = -0.26

¿A qué probabilidad (p_B) de lluvia para la playa estaríamos indiferente entre las dos opciones?

p_B * -0.6 = -0.26

p_B = -0.26 / -0.6 = 0.43

¿A qué probabilidad (p_B) de lluvia para la playa estaríamos indiferente entre las dos opciones?

Cuando la probabilidad de lluvia en la playa es del 43% (la probabilidad de lluvia en casa se mantiene en el 30%), nos resulta igual quedarnos en casa e ir a la playa.

Si la probabilidad de que llueva en la playa es > > del 43%, nos quedaríamos en casa.

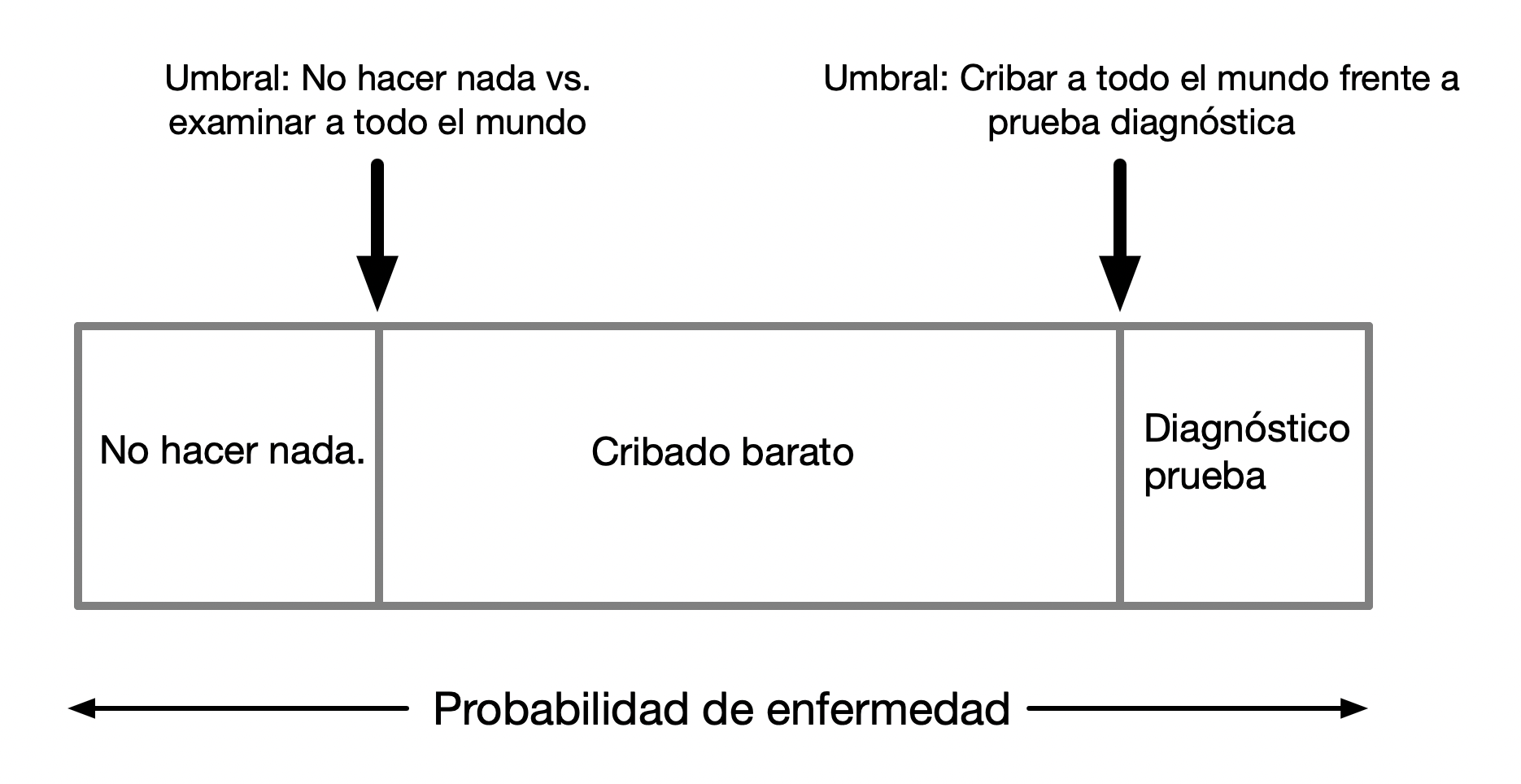
Ejemplo de umbral: Programa de cribado

Árbol de decisión: Embolia pulmonar

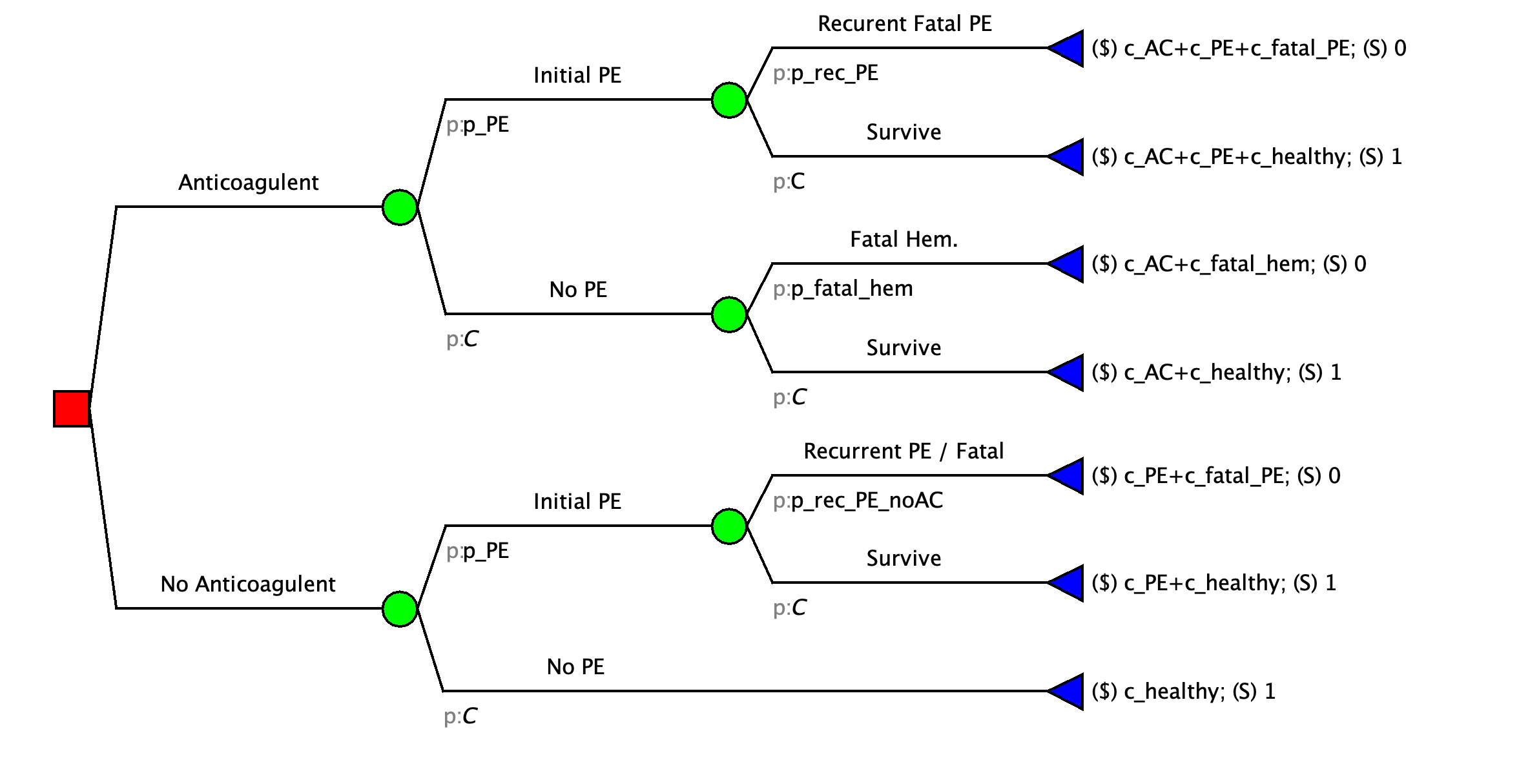
Árbol de decisión: Embolia pulmonar

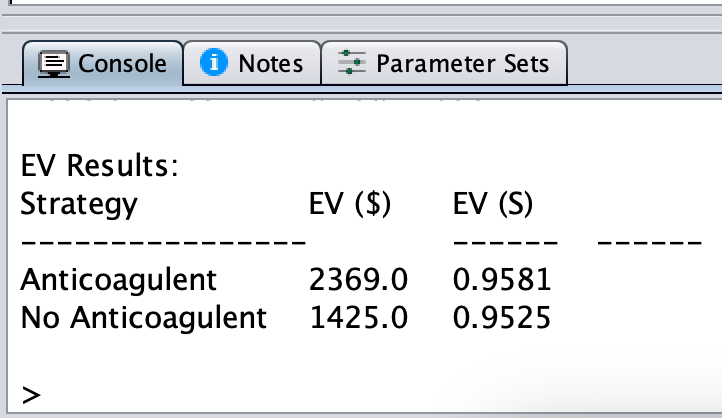
Incertidumbre de los parámetros

• Supongamos que no estamos seguros de la probabilidad de una fatal.

• ¿A qué valor de p_hem_fatal sería igual la supervivencia esperada?

Análisis de umbrales: Idea

• Permita que el valor de p_fatal_hem varíe en un intervalo.

• Encuentre el valor de p_fatal_hem a lo largo de este rango donde la supervivencia esperada supervivencia esperada es igual para las estrategias “Anticoagulante” y “Sin anticoagulante”. estrategias.

Análisis de umbrales

Análisis de umbrales

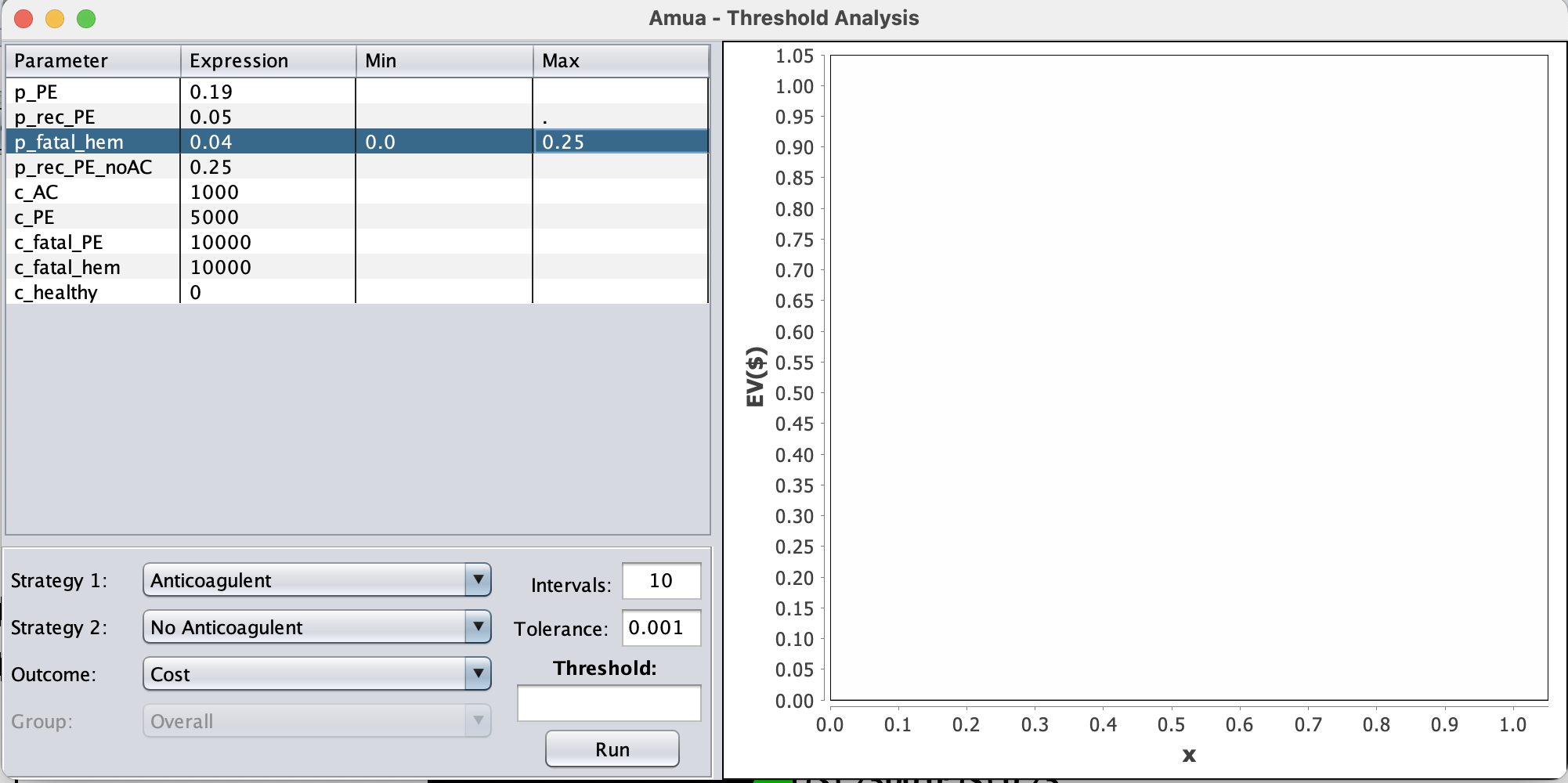
Threshold Analysis

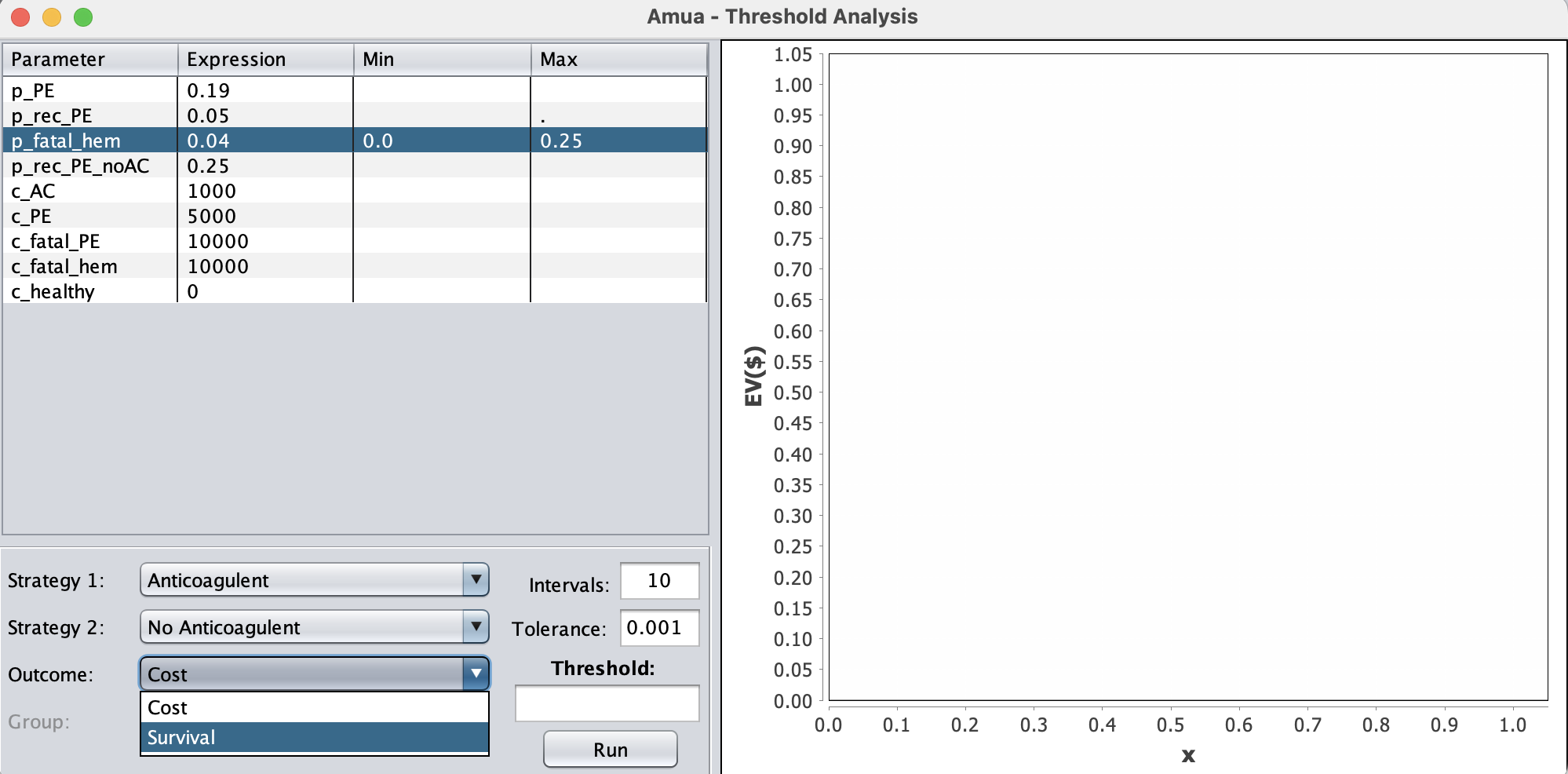
Análisis de umbrales

Análisis de umbrales

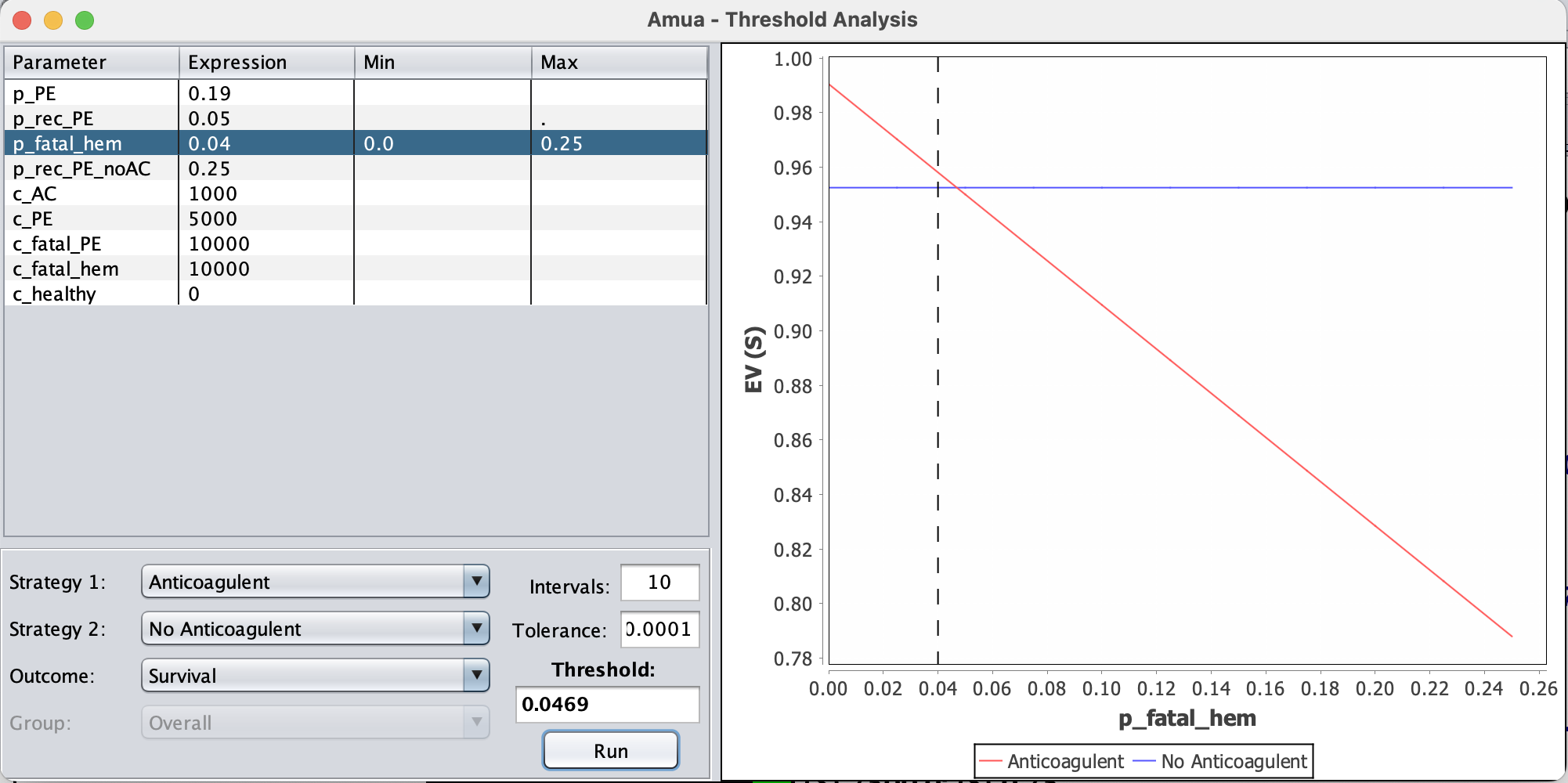
Ejemplo 2: Programa de detección

Programa de cribado

• El Ministerio de Sanidad está considerando la implantación de un programa de tratamiento para toda la población de una enfermedad costosa que afecta a un subgrupo de la población.
• La prevalencia de la enfermedad no está bien establecida.

Programa de detección

• Se dispone de una prueba de cribado barata, pero no es perfecta para detectar a los individuos con la enfermedad. detectar individuos con la enfermedad.
• Se dispone de una prueba diagnóstica más cara (perfecta).

Problema de decisión

1. No hacer nada.
2. Cribado poblacional con la prueba barata.
3. Prueba diagnóstica cara para todos.

Problema de decisión

• Dado que no conocemos la probabilidad subyacente de enfermedad (p_enfermedad), ¿podemos tomar una decisión política?
• Tal vez. Podemos utilizar un análisis de umbrales.

Análisis de umbrales: Pasos

1. Permitir que p_enfermedad varíe en un rango plausible.
2. Encontrar el umbral en el que nos sería indiferente entre:

• No hacer nada vs. cribado poblacional con prueba barata.
• Cribado de la población o prueba diagnóstica para todos.

Análisis del umbral