Modelos de Markov

Objetivos de aprendizaje y esquema

Objetivos de aprendizaje

  • Discutir las ventajas y desventajas de la modelización de decisiones mediante árboles de decisión frente a un modelo determinista formal

  • Comprender los componentes y la estructura de los modelos de Markov de tiempo discreto

  • Calcular los ciclos de Markov a mano, utilizando el diagrama de burbujas de Markov

  • Aplicar métodos de corrección de ciclos de Markov

Un proceso de enfermedad simple

  • Supongamos que queremos modelizar la razón costo-efectividad de estrategias alternativas para prevenir una enfermedad.
  • Partimos de una población sana de 25 años y existen tres estados de salud que pueden experimentar las personas:

    1. Permanecer sano.

    2. Enfermarse**.

    3. Morir

Un proceso de enfermedad simple

  • Permanecer sano no conlleva disminución de utilidad (peso de utilidad = 1,0 por ciclo en estado sano)
  • Enfermarse conlleva una disminución de utilidad de 0,25 durante el resto de la vida de la persona (peso de utilidad = 0,75).
  • La muerte conlleva un valor de utilidad de 0.

Un proceso de enfermedad simple

  • Permanecer sano no tiene ningún costo.
  • Enfermarse supone un costo de 1.000 $ al año.
  • Enfermarse aumenta el riesgo de muerte en un 300%.

Un proceso de enfermedad simple

El Instituto de Salud de un país estudia cinco estrategias de prevención que reducen el riesgo de enfermarse:

Estrategia Descripción Costo
A Normas de asistencia 25 $/año
B Reducción adicional del 4% del riesgo de enfermarse 1,000 $/año
C 12% de reducción del riesgo 3,100 $/año
D 8% de reducción del riesgo 1,550 $/año
E 8% de reducción del riesgo 5,000 $/año

Opción de modelo 1: Árbol de decisión

  • Una opción sería utilizar un árbol de decisión para modelar la utilidad esperada y los costos asociados a cada estrategia.
  • Horizonte temporal del modelo: 10 años
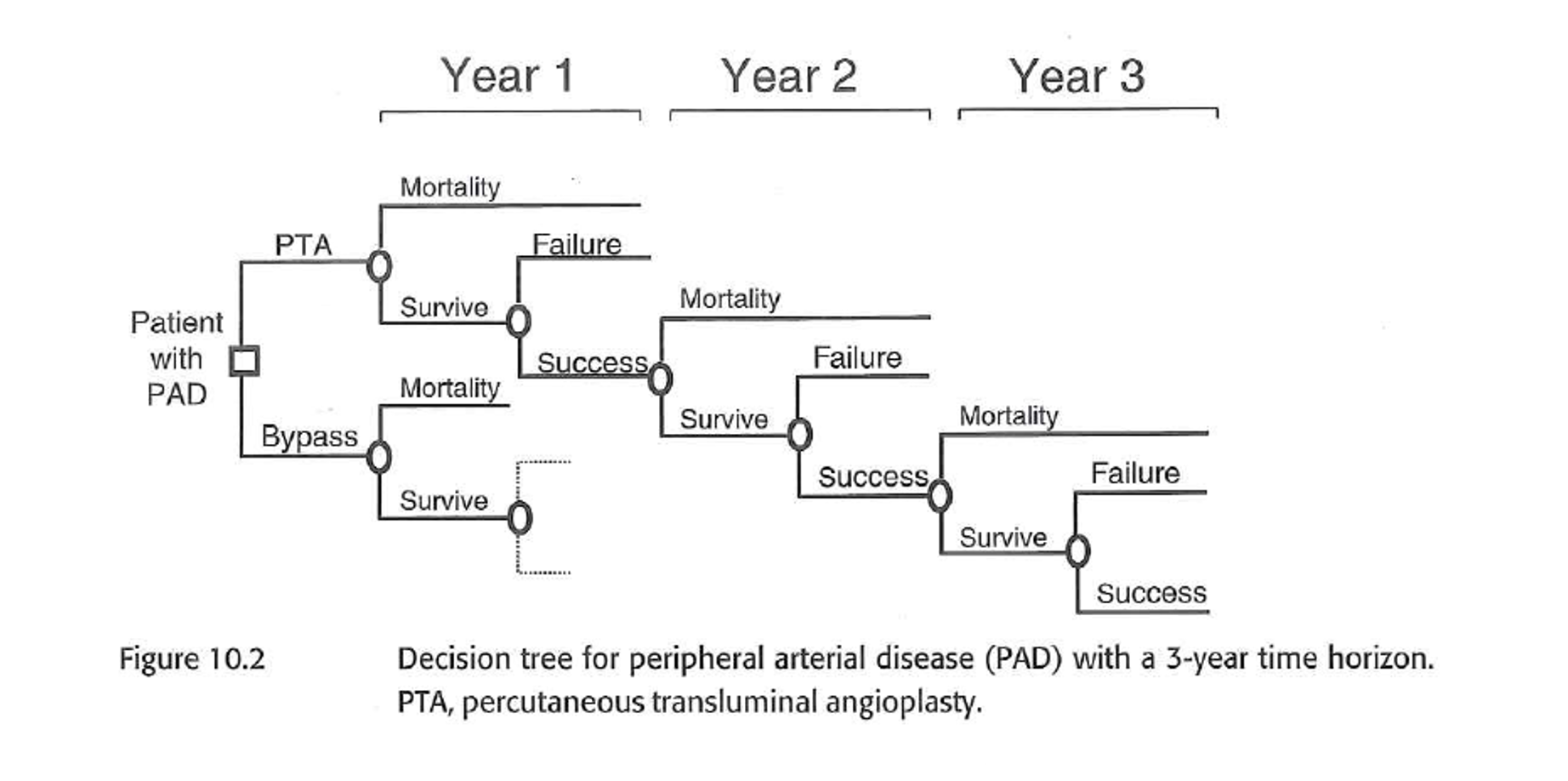
  • La siguiente diapositiva muestra el árbol de decisión para los resultados experimentados en el primer año.

Opción de modelo 1: Árbol de decisión

  • ¿Qué limitaciones ve?

Árbol de decisión para dos ciclos completos.

Estrategia Un árbol de decisión para 5 ciclos.

Árboles de decisión

Pros Contras
Sencillo, rápido y puede aportar información

Árboles de decisión

Pros Contras
Sencillo, rápido y puede aportar información
Fácil de describir y comprender

Árboles de decisión

Pros Contras
Sencillo, rápido y puede aportar información
Fácil de describir y comprender
Funciona bien con un horizonte temporal limitado

Árboles de decisión

Pros Contras
Sencillo, rápido y puede aportar información Difícil incluir detalles clínicos
Fácil de describir y comprender
Funciona bien con un horizonte temporal limitado

Árboles de decisión

Pros Contras
Sencillo, rápido y puede aportar información Difícil incluir detalles clínicos
Fácil de describir y comprender El paso del tiempo no es fácilmente evidente
Funciona bien con un horizonte temporal limitado

Árboles de decisión

Pros Contras
Sencillo, rápido y puede aportar información Difícil incluir detalles clínicos
Fácil de describir y comprender El paso del tiempo no es fácilmente evidente
Funciona bien con un horizonte temporal limitado Difícil modelizar horizontes temporales más largos (>1 ciclo)

Árboles de decisión

Próximos pasos

  • Idealmente, queremos un enfoque de modelado que pueda incorporar flexibilidad y manejar las complejidades que hacen que los árboles de decisión sean difíciles de manejar.

Modelos de Markov

Modelos de Markov

Enfoque habitual en los análisis de decisiones que añade flexibilidad adicional.

Pros Contras
Puede modelar sucesos repetidos

Modelos de Markov

Enfoque habitual en los análisis de decisiones que añade flexibilidad adicional.

Pros Contras
Puede modelar sucesos repetidos
Puede modelizar eventos clínicos más complejos y longitudinales

Modelos de Markov

Enfoque habitual en los análisis de decisiones que añade flexibilidad adicional.

Pros Contras
Puede modelar sucesos repetidos
Puede modelizar eventos clínicos más complejos y longitudinales
No requiere muchos cálculos; es eficiente de modelar y depurar.

Modelos de Markov

  • Las ventajas de los modelos de Markov se derivan de su estructura en torno a estados de enfermedad mutuamente excluyentes.

  • Estos estados de enfermedad representan los posibles estados o consecuencias de las estrategias u opciones consideradas.

  • Como hay un número fijo de estados de enfermedad en los que puede encontrarse la población, no es necesario modelar vías complejas, como vimos en la “explosión” del árbol de decisión hace unas diapositivas.

Árboles de Markov

También es habitual emparejar un modelo de Markov con un árbol de decisión1.

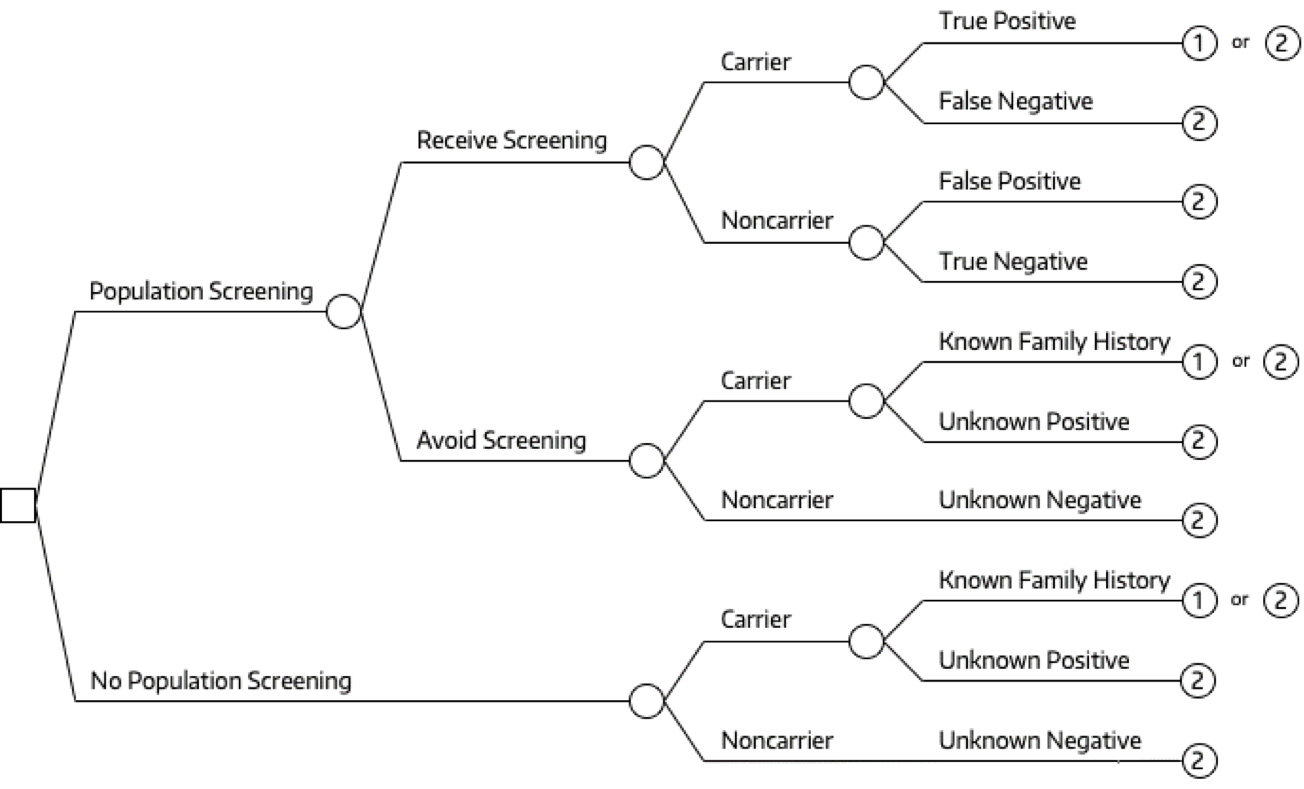
Árboles de Markov

También es habitual emparejar un modelo de Markov con un árbol de decisión1.

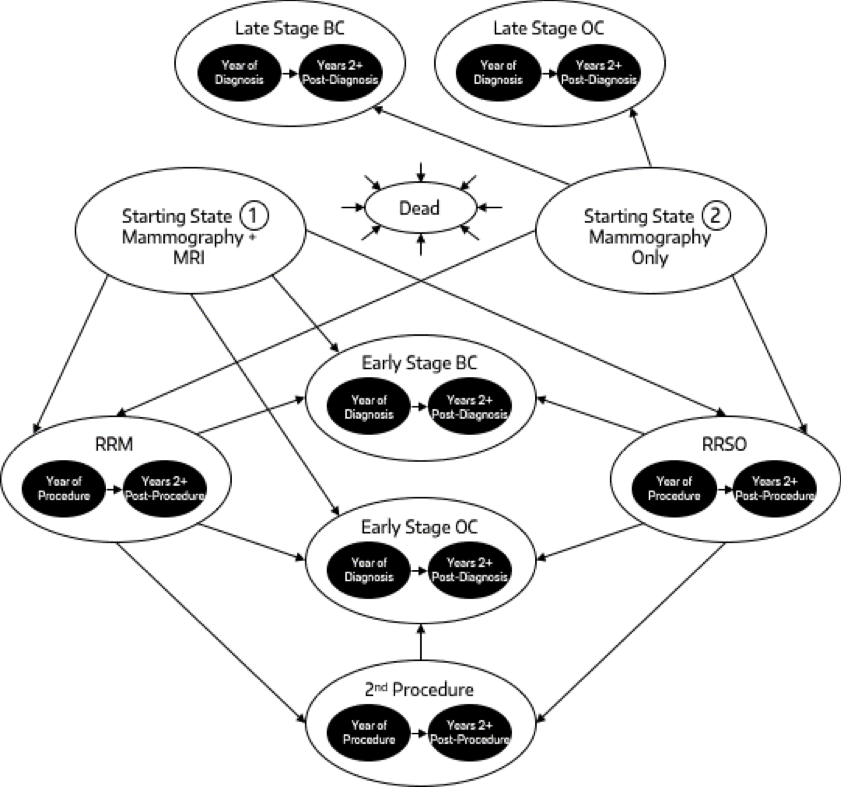
Árboles de Markov

Un árbol de decisión simple está implícito en casi todos los análisis de decisiones.

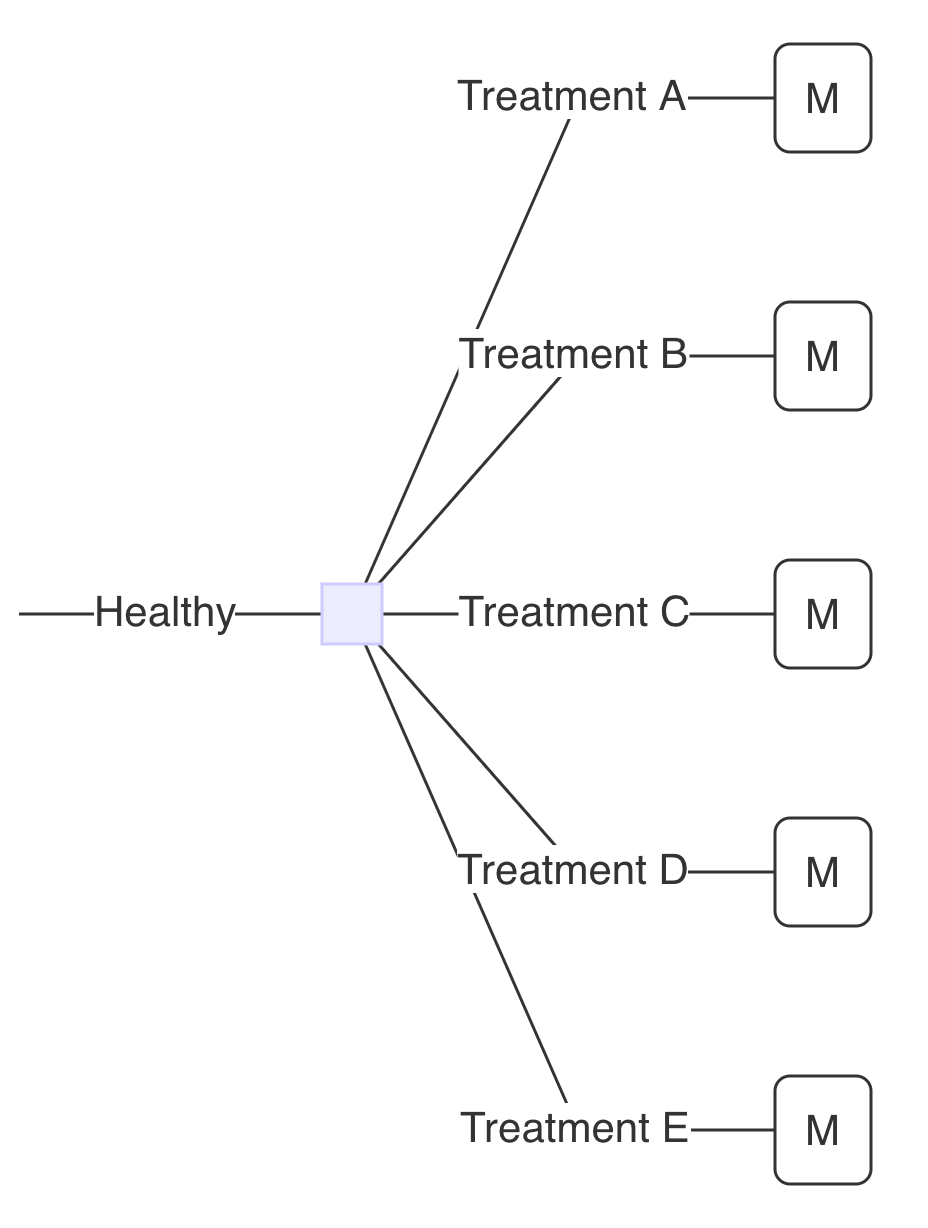
Árbol de Markov: Ejemplo

Tratamiento A: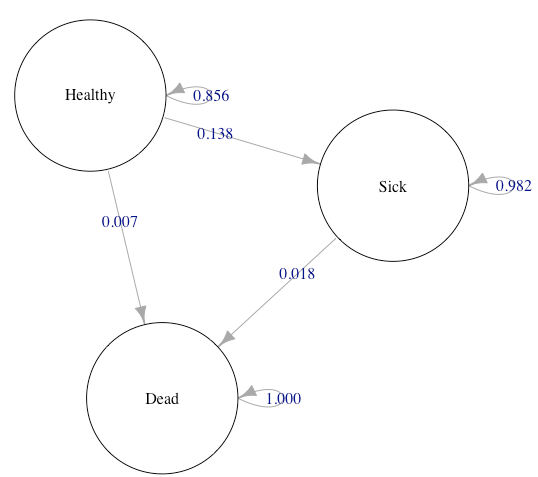

Árbol de Markov: Ejemplo

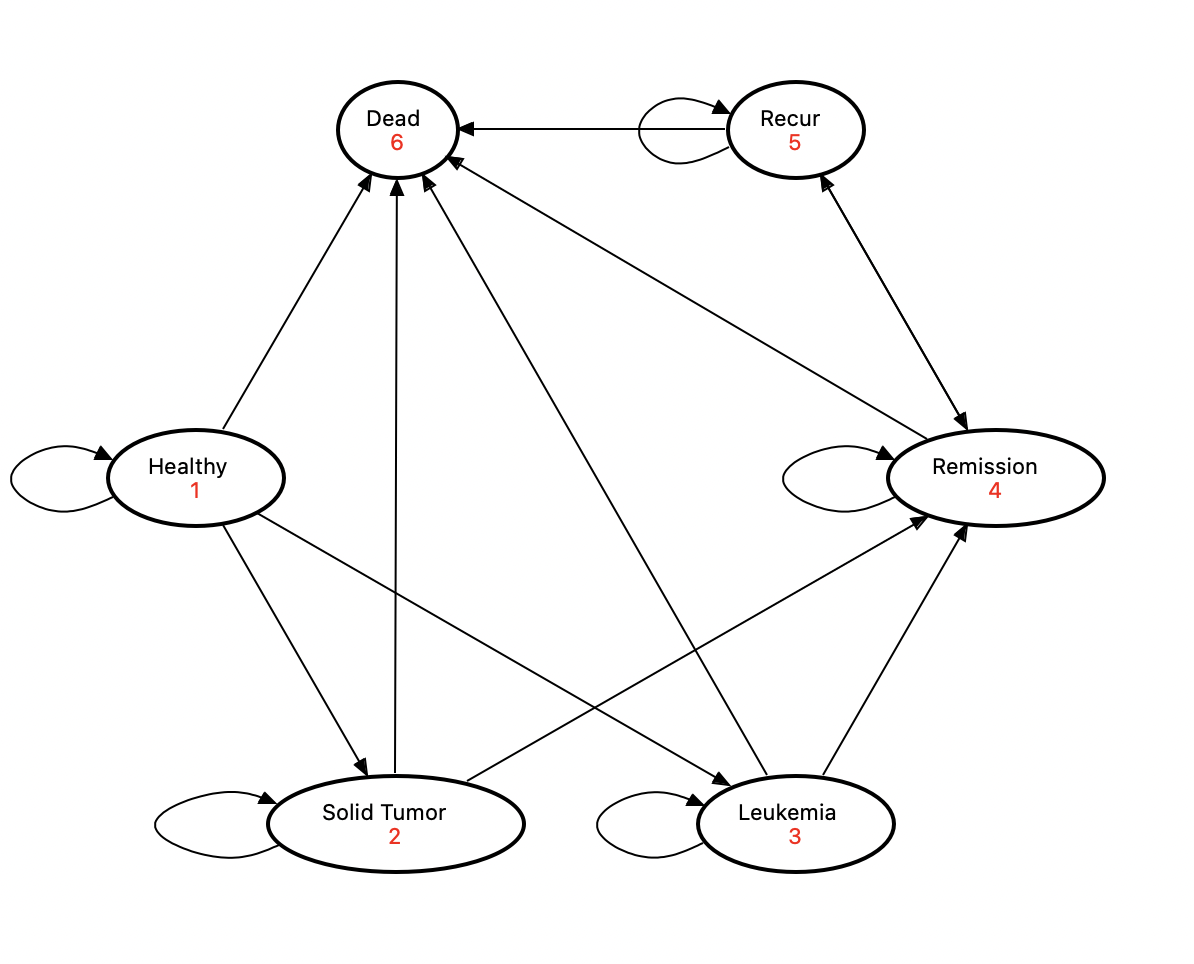
Tratamiento A: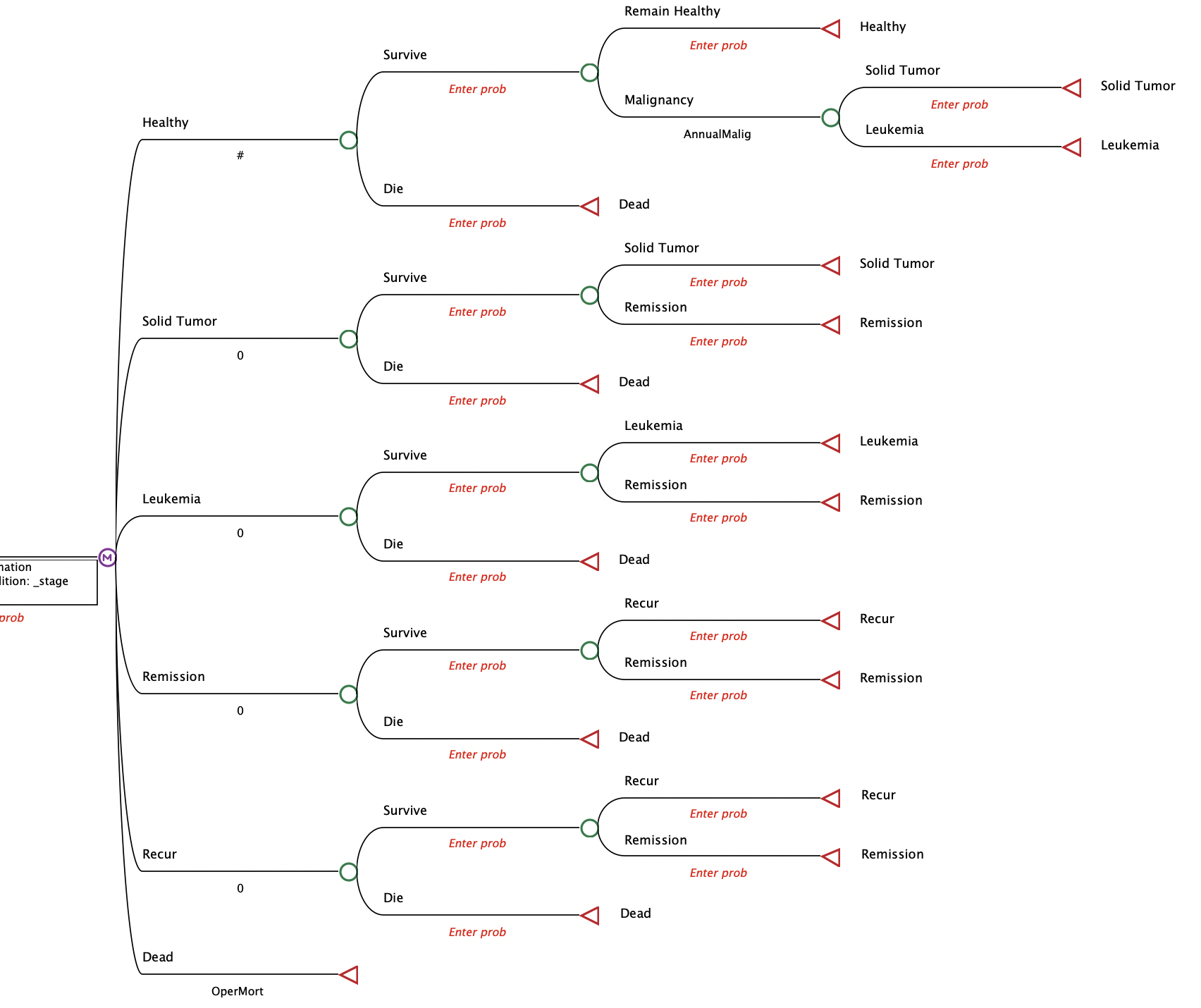

Al elegir una estructura de modelo…


“Las cosas deben hacerse tan simples como sea posible, pero no más simples” - Albert Einstein

Construir un Modelo Markov

Características principales

  • Permite transiciones de estado de salud en tiempo
  • Los individuos sólo pueden existir en un estado a la vez (estados de salud mutuamente excluyentes)
  • Al principio o al final de cada ciclo, los pacientes pasan por estados de salud mediante probabilidades de transición y los individuos permanecen en estado de salud durante el largo del ciclo
  • La probabilidad de transición depende del estado actual (“sin memoria”); (los estados túnel pueden tener en cuenta esta posible limitación)
  • Las probabilidades de transición permanecen constantes a lo largo del tiempo (aparte de las tablas de vida integradas)
  • Los resultados indican la “media” de la cohorte

Características principales


“CICLO” = Cantidad mínima de tiempo que cualquier individuo pasará en un estado antes de una posible transición a otro estado

  • Más información en las siguientes diapositivas

Pasos

  1. Definir el problema de decisión
  2. Conceptualizar el modelo
  3. Parametrizar el modelo
  4. Calcular o definir la matriz de probabilidades de transición
  5. Ejecutar el modelo

1. Definir el problema de decisión

Paso 1: Definir el problema de decisión

Ya hemos definido el problema de decisión anteriormente en este taller, así que repetiremos los objetivos básicos brevemente aquí.

Paso 1: Definir el problema de decisión

Objetivo: modelar la rentabilidad de estrategias alternativas para prevenir la aparición de una enfermedad.

Estrategia Descripción Costo
A Normas de asistencia 25 $/año
B Reducción adicional del 4% del riesgo de enfermarse 1,000 $/año
C 12% de reducción del riesgo 3,100 $/año
D 8% de reducción del riesgo 1,550 $/año
E 8% de reducción del riesgo 5,000 $/año

Paso 1: Definir el problema de decisión

2. Conceptualizar el modelo de Markov

2. Conceptualizar el modelo de Markov

Dos pasos principales:

2a. Determinar los estados de salud

2b. Determinar las transiciones

Paso 2: Conceptualizar el modelo

2a. Determinar estados de salud

  • Las personas pueden experimentar tres estados de salud:
    1. Permanecer Sano
    2. Enfermarse**.
    3. Morir

Paso 2: Conceptualizar el Modelo

2a. Determinar los estados de salud

  • Las personas pueden experimentar tres estados de salud:
    1. Permanecer Sano
    2. Enfermarse**.
    3. Morir

2b. Determinar transiciones

  • Los individuos que enferman no pueden volver a estar sanos.

“Diagrama de burbujas

Los diagramas de transición de estados (“burbuja”) son visualizaciones útiles de un modelo de Markov.

G Healthy Healthy Healthy->Healthy Sick Sick Healthy->Sick Dead Dead Healthy->Dead Sick->Sick Sick->Dead Dead->Dead

Diagram constructed using the Graphviz Visual Editor

3. Parametrizar el modelo

3. Parametrizar el modelo

Pasos básicos

3a. Determinar los parámetros básicos del modelo

3b. Seleccionar y definir las entradas del modelo

3. Parametrizar el modelo

Pasos básicos

3a. Determinar los parámetros básicos del modelo

  • Definir la población (por ejemplo, mujeres de 25 años)
  • Definir la duración del ciclo de Markov (por ejemplo, ciclo de 1 año)
  • Definir el horizonte temporal (p. ej., seguimiento hasta los 100 años o la muerte)

3a. Definir la longitud del ciclo de Markov

  • Fundamentalmente, estamos modelando un proceso de tiempo continuo (por ejemplo, progresión de la enfermedad).
  • Un modelo de Markov de tiempo discreto “divide” el tiempo en “trozos” (es decir, “ciclos”).
  • Una consecuencia es que el modelo nos mostrará qué fracción empieza un ciclo en un estado determinado y qué fracción termina en cada estado al final del ciclo.

3a. Definir la longitud del ciclo de Markov

  • Supongamos que utilizamos un ciclo de un año para el modelo sano-enfermo-muerto.
  • Pensemos en el proceso de enfermedad subyacente (en tiempo continuo).
    • Recordemos que enfermar aumenta sustancialmente la probabilidad de morir.
  • Si no tenemos cuidado, ¿qué estamos suponiendo (implícitamente) que puede y puede y no puede ocurrir en un solo ciclo?

3a. Definir la longitud del ciclo de Markov

3a. Definir la longitud del ciclo de Markov

El reto de seleccionar una longitud de ciclo adecuada se reduce a cómo tratamos los riesgos en competencia.

  • Riesgos concurrentes: los individuos pueden pasar de su estado de salud actual a otros dos o más estados de salud.

G Healthy Healthy Healthy->Healthy Sick Sick Healthy->Sick Dead Dead Healthy->Dead Sick->Sick Sick->Dead Dead->Dead

3a. Definir la longitud del ciclo de Markov

El reto de seleccionar una duración de ciclo adecuada se reduce a cómo manejamos los riesgos en competencia.

  • Si no tenemos cuidado, podríamos descartar la posibilidad… de la Sano Enfermo Muerto dentro de un ciclo.
  • El modelo sería como una transición Sano Muerto básico, pero se desvió a través de Enfermo en el camino.

G Healthy Healthy Healthy->Healthy Sick Sick Healthy->Sick Dead Dead Healthy->Dead Sick->Sick Sick->Dead Dead->Dead

3a. Definir la longitud del ciclo de Markov

Pros Contras
Puede modelar sucesos repetidos Sólo puede transitar una vez por ciclo
Puede modelizar eventos clínicos más complejos y longitudinales
No requiere muchos cálculos; es eficiente de modelar y depurar.

3a. Definir la longitud del ciclo de Markov

  • Puede resultar tentador simplemente acortar la duración del ciclo (por ejemplo, utilizar un ciclo de 1 día frente a 1 año).

incremental - Para un horizonte de 75 años, ¿cuántos ciclos serían? - ¡¡¡- 27,375!!! - ¿Hay algún problema? :::

3a. Definir la longitud del ciclo de Markov

  • Acortar el ciclo supone un reto computacional.
  • El caso base requiere 27.375 ciclos diarios.
  • Supongamos ahora que queremos realizar 2.000 análisis de sensibilidad probabilística probabilístico.
    • Ahora tenemos que hacer frente a 57.750.000 ciclos.

3a. Definir la longitud del ciclo de Markov

Pros Contras
Puede modelar sucesos repetidos Sólo puede transitar una vez por ciclo
Puede modelizar eventos clínicos más complejos y longitudinales Acortar el ciclo puede plantear retos informáticos.
No requiere muchos cálculos; es eficiente de modelar y depurar.

3a. Definir la longitud del ciclo de Markov

Más retos …

3a. Definir la longitud del ciclo de Markov

Más retos …

  • Los modelos de Markov carecen de memoria: no recuerdan lo que ocurrió antes del ciclo actual.
    • Si su riesgo de transición a un estado de salud más grave depende de de acontecimientos anteriores, el modelo no puede tenerlo en cuenta explícitamente.

3a. Definir la longitud del ciclo de Markov

Más retos …

  • Existen soluciones conocidas como “estados túnel” para evitar este problema, aunque son difíciles de hacer y presentan sus propios problemas
    • No los trataremos esta semana, pero podemos proporcionar referencias si quieren explorar.

3a. Definir la longitud del ciclo de Markov

Pros Contras
Puede modelar sucesos repetidos Sólo puede transitar una vez por ciclo
Puede modelizar eventos clínicos más complejos y longitudinales Acortar el ciclo puede plantear retos informáticos.
No requiere muchos cálculos; es eficiente de modelar y depurar. Acortar el ciclo puede provocar una “explosión de estados” si se utilizan estados túnel

3a. Definir la longitud del ciclo de Markov

  • También es aconsejable elegir una duración de ciclo que se alinee con los los plazos clínicos/enfermedad del problema de decisión.
    • Esquemas de tratamiento.
    • Enfermedad aguda frente a crónica.
  • Otra opción es incorporar los acontecimientos “a corto plazo” que se producen en el curso de una enfermedad/intervención dentro del árbol de decisión y, a continuación, permitir que el modelo de Markov modele las consecuencias sanitarias a largo plazo.

G Healthy Healthy Healthy->Healthy Sick Sick Healthy->Sick Dead Dead Healthy->Dead Sick->Sick Sick->Dead Dead->Dead

3. Parametrizar el modelo

3b. Seleccionar y definir las entradas del modelo

  • 3b.i. Fuente y definir el caso base valores.

  • 3b.ii. Origen y definición de las fuentes de incertidumbre.

3. Parametrizar el modelo

3b. Seleccionar y definir las entradas del modelo

  • Tasa de incidencia de la enfermedad
  • Utilidades y costos del estado de salud
  • Relaciones de riesgo, odds ratios o riesgos relativos para diferentes estrategias.
  • … y así sucesivamente.

3. Parametrizar el modelo

Hemos definido muchos de los parámetros subyacentes antes en este taller, por lo que los repetiremos brevemente aquí.

3. Parametrizar el modelo

  • Comenzamos con una población sana de 25 años de edad y los seguimos hasta los 100 años (o la muerte, si es antes).
  • Permanecer sano no conlleva ninguna disminución de la utilidad (peso de la utilidad= 1,0)
  • Enfermarse conlleva una disminución de la utilidad de 0,25 durante el resto de la vida de la persona (peso de utilidad = 0,75)
  • La muerte tiene un peso de utilidad de 0.

3. Parametrizar el modelo

  • No hay ningún costo asociado a mantenerse sano.
  • Enfermar supone un costo de 1.000 $/año.
  • Enfermar aumenta el riesgo de muerte en un 300%.

3. Parametrizar el modelo

Cada estrategia tiene un costo y un impacto diferente en la probabilidad de enfermar.

Estrategia Descripción Costo
A Normas de asistencia 25 $/año
B Reducción adicional del 4% del riesgo de enfermar 1,000 $/año
C 12% de reducción del riesgo 3,100 $/año
D 8% de reducción del riesgo 1,550 $/año
E 8% de reducción del riesgo 5,000 $/año

3. Parametrizar el modelo

Es crítico seguir un proceso formal para parametrizar su modelo.

  • A menudo, los parámetros se extraen de la literatura publicada, y es importante rastrear la fuente (valor publicado, suposición, etc.) de cada parámetro del modelo.
    • Por ejemplo, el parámetro de reducción porcentual del riesgo de cada estrategia puede proceder de distintos ensayos clínicos.
    • El parámetro que rige la muerte por causas de fondo puede derivarse de datos de mortalidad.

3. Parametrizar el modelo

Es crítico seguir un proceso formal para parametrizar su modelo.

  • Algunos parámetros pueden ser simplemente valores (por ejemplo, el costo de la estrategia A es de \25 $/año)
  • Algunos parámetros pueden ser funciones de otros parámetros.
    • Por ejemplo, supongamos que queremos seguir a una cohorte de personas de 25 años hasta los 100 años o la muerte, si ésta se produce antes.
    • En ese caso tenemos dos parámetros “fijos”: la edad inicial y la edad máxima.
    • Podemos utilizar estos dos parámetros para deducir el número total de ciclos que necesitamos realizar.

3. Parametrizar el modelo

Es crítico seguir un proceso formal para parametrizar su modelo.

  • Los parámetros también tienen varios “sabores”:
    1. Probabilidades
    2. Tasas
    3. Relaciones de riesgo
    4. Costos
    5. Utilidades
    6. etc.

3. Parametrizar el modelo

Es crítico seguir un proceso formal para parametrizar su modelo.

  • Todo lo anterior resalta la importancia de adoptar un proceso formal para nombrar y rastrear el valor, la fuente y la distribución de incertidumbre de todos los parámetros del modelo en un único lugar.

  • Recomendamos un enfoque estructurado basado en convenciones de nomenclatura de parámetros y tablas de parámetros.

3. Parametrizar el modelo

Convenciones de nomenclatura:

type prefix
Probabilidad p_
Tasa (Rate) r_
Matriz m_
Costo c_
Utilidad u_
Razón de riesgo (hazard ratio) hr_

Tabla de parámetros

::: pie de página Nota: En la tabla sólo se muestra un subconjunto de parámetros del modelo. :::

Tabla de parámetros
param base_case formula description notes distribution source
n_age_init 25.00
Age at baseline

Modeling Parameter
n_age_max 100.00
Maximum age of followup

Modeling Parameter
u_H 1.00
Utility weight of healthy (H)
beta(shape1 = 200, shape2 = 3) Leech et al. (2022)
u_S 0.75
Utility weight of sick (S)
beta(shape1 = 130, shape2 = 45) Leech et al. (2022)
c_S 1000.00
Annual cost of sick (S)
gamma(shape = 44.4, scale = 22.5) Graves et al. (2022)
c_trtA 25.00
Cost of treatment A
gamma(shape = 12.5, scale = 2) Martin et al. (2022)
c_trtB 1000.00
Cost of treatment B
gamma(shape = 12, scale = 83.3) Assumption
c_trtC 3100.00
Cost of treatment C
gamma(shape = 36.144, scale = 83) Assumption
n_cycles 75.00 (n_age_max - n_age_init) Time horizon


param columna es el nombre corto del parámetro

Nota: En la tabla sólo se muestra un subconjunto de parámetros del modelo.

Tabla de parámetros
param base_case formula description notes distribution source
n_age_init 25.00
Age at baseline

Modeling Parameter
n_age_max 100.00
Maximum age of followup

Modeling Parameter
u_H 1.00
Utility weight of healthy (H)
beta(shape1 = 200, shape2 = 3) Leech et al. (2022)
u_S 0.75
Utility weight of sick (S)
beta(shape1 = 130, shape2 = 45) Leech et al. (2022)
c_S 1000.00
Annual cost of sick (S)
gamma(shape = 44.4, scale = 22.5) Graves et al. (2022)
c_trtA 25.00
Cost of treatment A
gamma(shape = 12.5, scale = 2) Martin et al. (2022)
c_trtB 1000.00
Cost of treatment B
gamma(shape = 12, scale = 83.3) Assumption
c_trtC 3100.00
Cost of treatment C
gamma(shape = 36.144, scale = 83) Assumption
n_cycles 75.00 (n_age_max - n_age_init) Time horizon


base_case es el valor del parámetro para el caso base.

Nota: En la tabla sólo se muestra un subconjunto de parámetros del modelo.

Tabla de parámetros
param base_case formula description notes distribution source
n_age_init 25.00
Age at baseline

Modeling Parameter
n_age_max 100.00
Maximum age of followup

Modeling Parameter
u_H 1.00
Utility weight of healthy (H)
beta(shape1 = 200, shape2 = 3) Leech et al. (2022)
u_S 0.75
Utility weight of sick (S)
beta(shape1 = 130, shape2 = 45) Leech et al. (2022)
c_S 1000.00
Annual cost of sick (S)
gamma(shape = 44.4, scale = 22.5) Graves et al. (2022)
c_trtA 25.00
Cost of treatment A
gamma(shape = 12.5, scale = 2) Martin et al. (2022)
c_trtB 1000.00
Cost of treatment B
gamma(shape = 12, scale = 83.3) Assumption
c_trtC 3100.00
Cost of treatment C
gamma(shape = 36.144, scale = 83) Assumption
n_cycles 75.00 (n_age_max - n_age_init) Time horizon


formula define fórmulas de parámetros del modelo para parámetros que son funciones de otros parámetros del modelo.

Nota: En la tabla sólo se muestra un subconjunto de parámetros del modelo.

Tabla de parámetros
param base_case formula description notes distribution source
n_age_init 25.00
Age at baseline

Modeling Parameter
n_age_max 100.00
Maximum age of followup

Modeling Parameter
u_H 1.00
Utility weight of healthy (H)
beta(shape1 = 200, shape2 = 3) Leech et al. (2022)
u_S 0.75
Utility weight of sick (S)
beta(shape1 = 130, shape2 = 45) Leech et al. (2022)
c_S 1000.00
Annual cost of sick (S)
gamma(shape = 44.4, scale = 22.5) Graves et al. (2022)
c_trtA 25.00
Cost of treatment A
gamma(shape = 12.5, scale = 2) Martin et al. (2022)
c_trtB 1000.00
Cost of treatment B
gamma(shape = 12, scale = 83.3) Assumption
c_trtC 3100.00
Cost of treatment C
gamma(shape = 36.144, scale = 83) Assumption
n_cycles 75.00 (n_age_max - n_age_init) Time horizon


description proporciona una descripción de texto del parámetro.

Tabla de parámetros
param base_case formula description notes distribution source
n_age_init 25.00
Age at baseline

Modeling Parameter
n_age_max 100.00
Maximum age of followup

Modeling Parameter
u_H 1.00
Utility weight of healthy (H)
beta(shape1 = 200, shape2 = 3) Leech et al. (2022)
u_S 0.75
Utility weight of sick (S)
beta(shape1 = 130, shape2 = 45) Leech et al. (2022)
c_S 1000.00
Annual cost of sick (S)
gamma(shape = 44.4, scale = 22.5) Graves et al. (2022)
c_trtA 25.00
Cost of treatment A
gamma(shape = 12.5, scale = 2) Martin et al. (2022)
c_trtB 1000.00
Cost of treatment B
gamma(shape = 12, scale = 83.3) Assumption
c_trtC 3100.00
Cost of treatment C
gamma(shape = 36.144, scale = 83) Assumption
n_cycles 75.00 (n_age_max - n_age_init) Time horizon


Nota: En la tabla sólo se muestra un subconjunto de parámetros del modelo.

notas es una columna opcional donde se añaden notas adicionales o contexto para el parámetro.

Nota: En la tabla sólo se muestra un subconjunto de parámetros del modelo.

Tabla de parámetros
param base_case formula description notes distribution source
n_age_init 25.00
Age at baseline

Modeling Parameter
n_age_max 100.00
Maximum age of followup

Modeling Parameter
u_H 1.00
Utility weight of healthy (H)
beta(shape1 = 200, shape2 = 3) Leech et al. (2022)
u_S 0.75
Utility weight of sick (S)
beta(shape1 = 130, shape2 = 45) Leech et al. (2022)
c_S 1000.00
Annual cost of sick (S)
gamma(shape = 44.4, scale = 22.5) Graves et al. (2022)
c_trtA 25.00
Cost of treatment A
gamma(shape = 12.5, scale = 2) Martin et al. (2022)
c_trtB 1000.00
Cost of treatment B
gamma(shape = 12, scale = 83.3) Assumption
c_trtC 3100.00
Cost of treatment C
gamma(shape = 36.144, scale = 83) Assumption
n_cycles 75.00 (n_age_max - n_age_init) Time horizon


distribución especifica la distribución de incertidumbre para el parámetro. Se utiliza para los análisis de sensibilidad probabilísticos.

Nota: En la tabla sólo se muestra un subconjunto de parámetros del modelo.

Tabla de parámetros
param base_case formula description notes distribution source
n_age_init 25.00
Age at baseline

Modeling Parameter
n_age_max 100.00
Maximum age of followup

Modeling Parameter
u_H 1.00
Utility weight of healthy (H)
beta(shape1 = 200, shape2 = 3) Leech et al. (2022)
u_S 0.75
Utility weight of sick (S)
beta(shape1 = 130, shape2 = 45) Leech et al. (2022)
c_S 1000.00
Annual cost of sick (S)
gamma(shape = 44.4, scale = 22.5) Graves et al. (2022)
c_trtA 25.00
Cost of treatment A
gamma(shape = 12.5, scale = 2) Martin et al. (2022)
c_trtB 1000.00
Cost of treatment B
gamma(shape = 12, scale = 83.3) Assumption
c_trtC 3100.00
Cost of treatment C
gamma(shape = 36.144, scale = 83) Assumption
n_cycles 75.00 (n_age_max - n_age_init) Time horizon


Nota: En la tabla sólo se muestra un subconjunto de parámetros del modelo.

source proporciona la fuente del parámetro. Puede ser un artículo de investigación publicado, una hipótesis o simplemente un parámetro de modelización sin (por ejemplo, la edad inicial de la cohorte modelada).

Tabla de parámetros
param base_case formula description notes distribution source
n_age_init 25.00
Age at baseline

Modeling Parameter
n_age_max 100.00
Maximum age of followup

Modeling Parameter
u_H 1.00
Utility weight of healthy (H)
beta(shape1 = 200, shape2 = 3) Leech et al. (2022)
u_S 0.75
Utility weight of sick (S)
beta(shape1 = 130, shape2 = 45) Leech et al. (2022)
c_S 1000.00
Annual cost of sick (S)
gamma(shape = 44.4, scale = 22.5) Graves et al. (2022)
c_trtA 25.00
Cost of treatment A
gamma(shape = 12.5, scale = 2) Martin et al. (2022)
c_trtB 1000.00
Cost of treatment B
gamma(shape = 12, scale = 83.3) Assumption
c_trtC 3100.00
Cost of treatment C
gamma(shape = 36.144, scale = 83) Assumption
n_cycles 75.00 (n_age_max - n_age_init) Time horizon


4. Calcular o definir la matriz de probabilidad de transición

Definición de la matriz de probabilidad de transición

  • La matriz de probabilidad de transición es una matriz cuadrada que define la probabilidad de transición de un estado de salud a otro estado de salud en un solo ciclo.

  • Construir la matriz es un proceso bastante técnico, pero bastante sencillo.

    • Podríamos dedicarle un día entero del taller y casos de estudio
    • Sin embargo, en aras del tiempo, vamos a pasar por alto estos detalles técnicos de hoy.

Matriz de probabilidades de transición

G Sano Sano Sano->Sano 0,856 Enfermo Enfermo Sano->Enfermo 0.138 Muerto Muerto Sano->Muerto 0.007 Enfermo->Enfermo 0.982 Enfermo->Muerto 0.018 Muerto->Muerto 1.0

Sano Enfermo Muerto
Sano 0.856 0.138 0.007
Enfermo 0 0.982 0.018
Muerto 0 0 1

5. Ejecutar el modelo

Ejecutar el modelo requiere dos entradas

Estado de salud al inicio del ciclo

Matriz de probabilidad de transición

Estado de salud al inicio del ciclo

Matriz de probabilidad de transición

Estado de salud al inicio del ciclo

Matriz de probabilidad de transición

\quad \quad \quad \quad \quad \quad \quad \quad

s =

 H S D
 1 0 0

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

\quad \quad \quad \quad

Estado de salud al inicio del ciclo

Matriz de probabilidades de transición

Estado de salud al final del ciclo

s =

 H S D
 1 0 0

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

s \cdot P=

     H     S     D
 0.856 0.138 0.007

Estado de salud al inicio del ciclo

Matriz de probabilidades de transición

Estado de salud al final del ciclo

s =

 H S D
 1 0 0

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

s \cdot P=

     H     S     D
 0.856 0.138 0.007

Estado de salud al inicio del ciclo

Matriz de probabilidades de transición

Estado de salud al final del ciclo

s =

 H S D
 1 0 0
     H     S     D
 0.856 0.138 0.007

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000
      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

s \cdot P=

     H     S     D
 0.856 0.138 0.007
     H     S     D
 0.733 0.254 0.015

Estado de salud al inicio del ciclo

Matriz de probabilidades de transición

Estado de salud al final del ciclo

s =

 H S D
 1 0 0
     H     S     D
 0.856 0.138 0.007
     H     S     D
 0.733 0.254 0.015

P =

      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000
      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000
      H     S     D
H 0.856 0.138 0.007
S 0.000 0.982 0.018
D 0.000 0.000 1.000

s \cdot P=

     H     S     D
 0.856 0.138 0.007
     H     S     D
 0.733 0.254 0.015
     H    S     D
 0.627 0.35 0.025

Estado de salud al final del ciclo

     H     S     D
 0.856 0.138 0.007
       H       S        D
 0.73274 0.25364 0.015476
       H      S        D
 0.62722 0.3502 0.025171

Rastreo de Markov

Estado de salud durante diez ciclos

 cycle       H       S        D
     0 1.00000 0.00000 0.000000
     1 0.85600 0.13800 0.007000
     2 0.73274 0.25364 0.015476
     3 0.62722 0.35020 0.025171
     4 0.53690 0.43045 0.035865
     5 0.45959 0.49679 0.047371
     6 0.39341 0.55127 0.059531
     7 0.33676 0.59564 0.072207
     8 0.28826 0.63139 0.085286
     9 0.24675 0.65981 0.098669
    10 0.21122 0.68198 0.112273

Calcular ciclos a mano

Ejemplo práctico

  • Se ha desarrollado un nuevo fármaco para pacientes con cáncer en remisión para disminuir su probabilidad de recaída
  • Este medicamento cuesta $10,000 por año (2022 USD)
  • Pregunta de investigación: ¿Es el nuevo fármaco rentable en comparación con el tratamiento estándar actual?
  • Supongamos que queremos modelizar esto en un horizonte temporal de 4 años

Ejemplo práctico


Standard of Care New Drug
Healthy to Stage 1 5%
Healthy to Stage 2 2%
Healthy to Stage 3 1%
Stage 1 to Stage 2 10%
Stage 1 to Remission 25%
Stage 2 to Stage 1 5%
Stage 2 to Stage 3 15%
Stage 2 to Remission 20%
Stage 3 to Stage 2 5%
Stage 3 to Death 45%
Remission to Stage 1 10% 2%
Remission to Stage 2 5% 1%

Ejemplo práctico

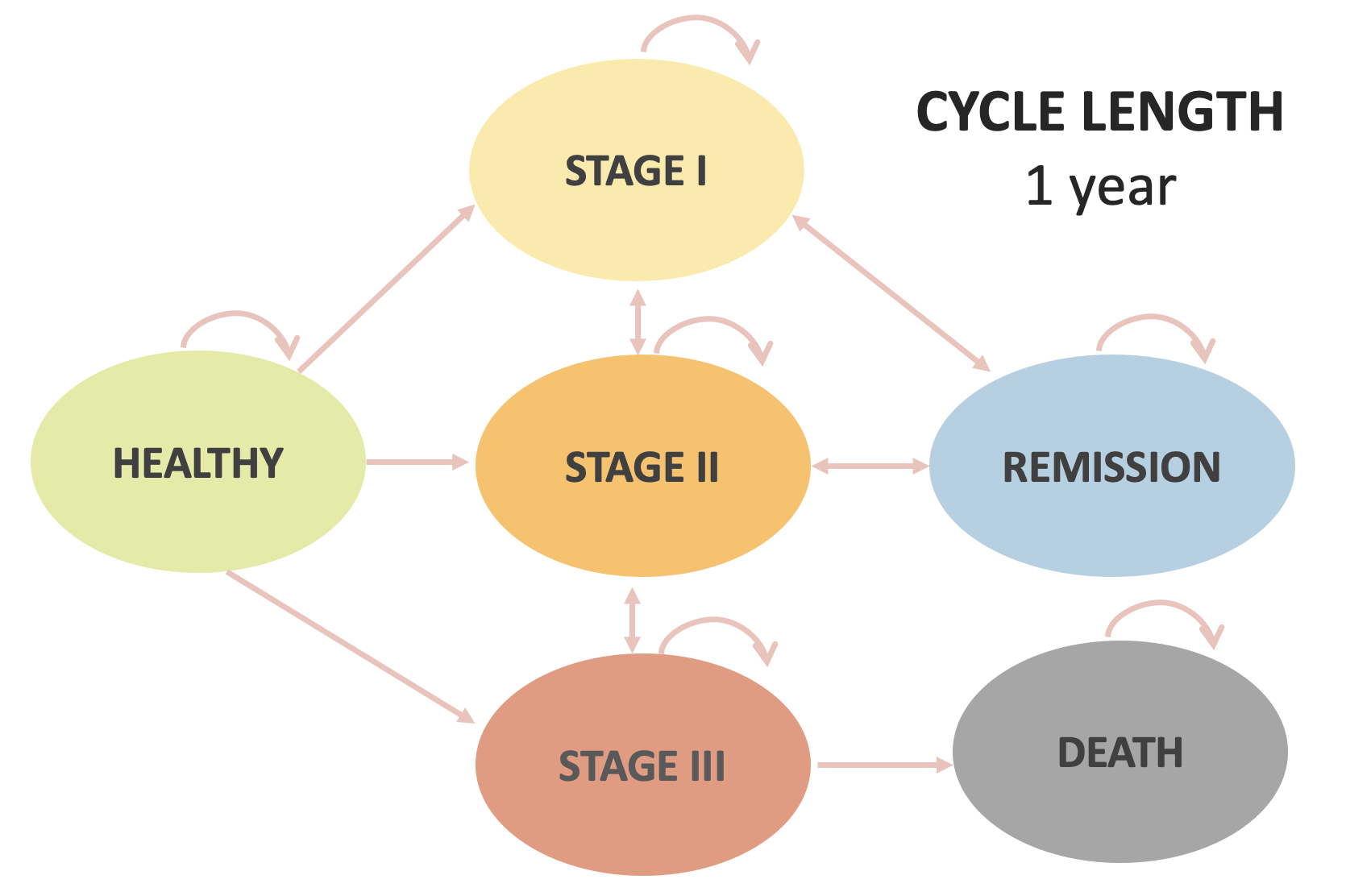
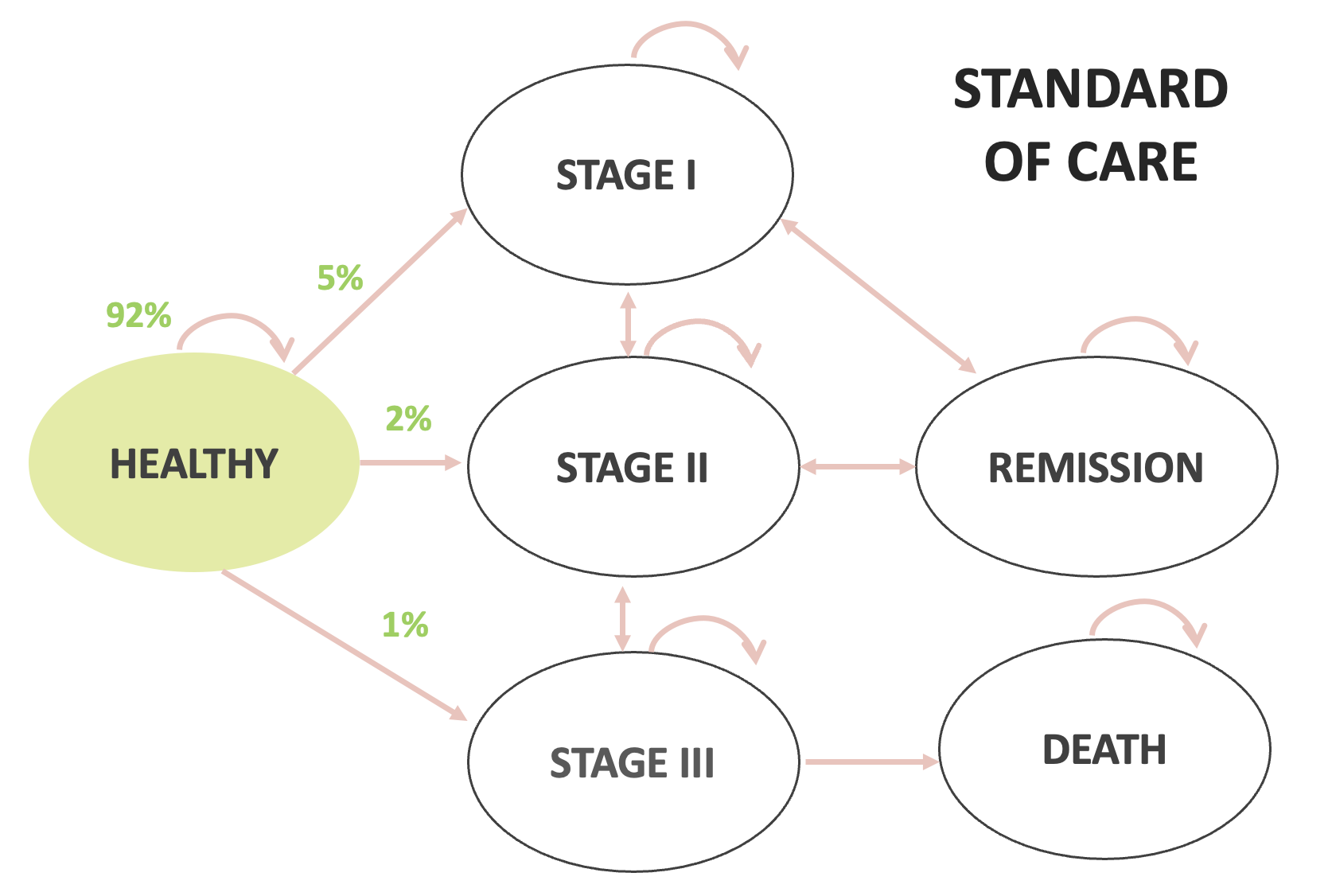
Ejemplo práctico

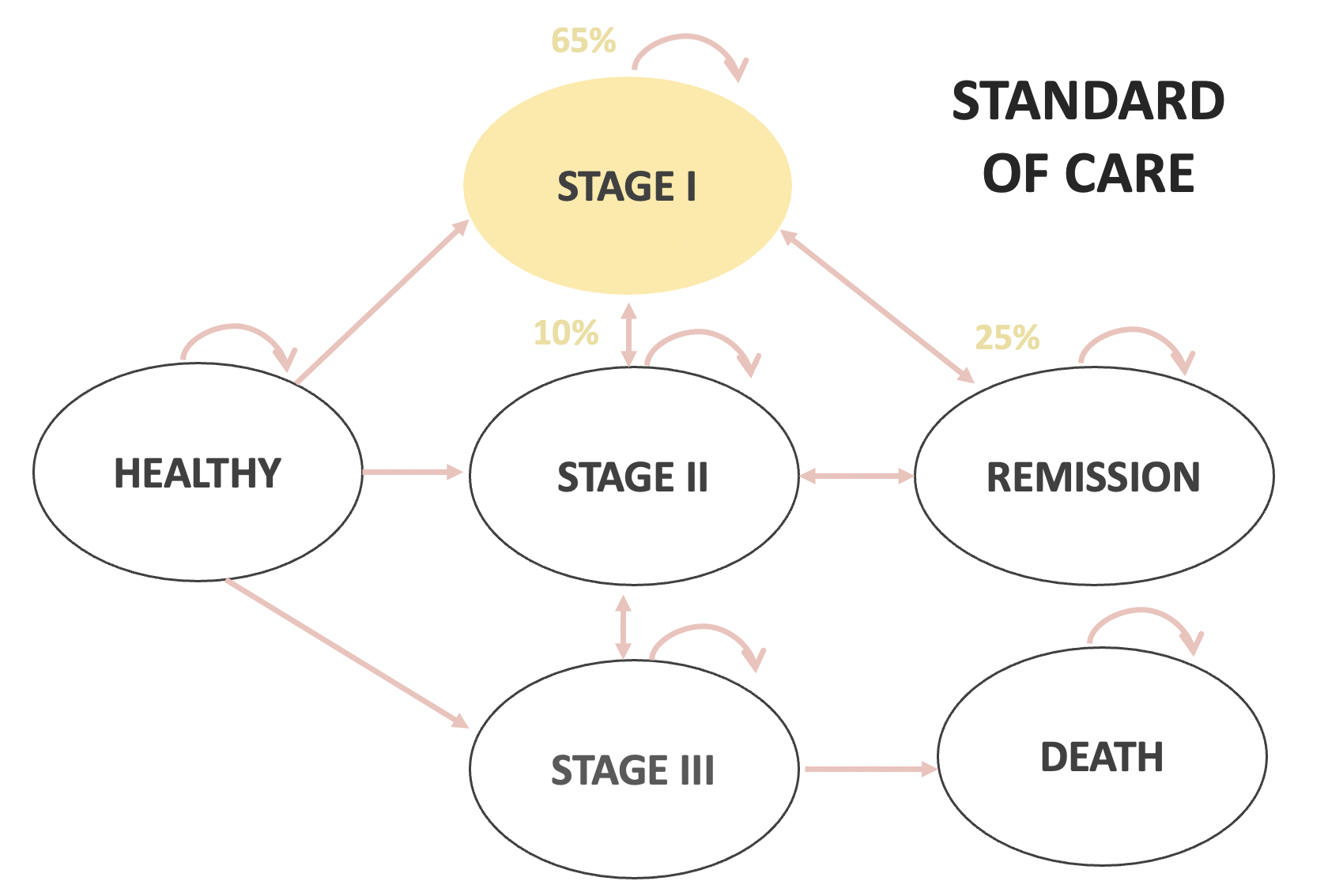
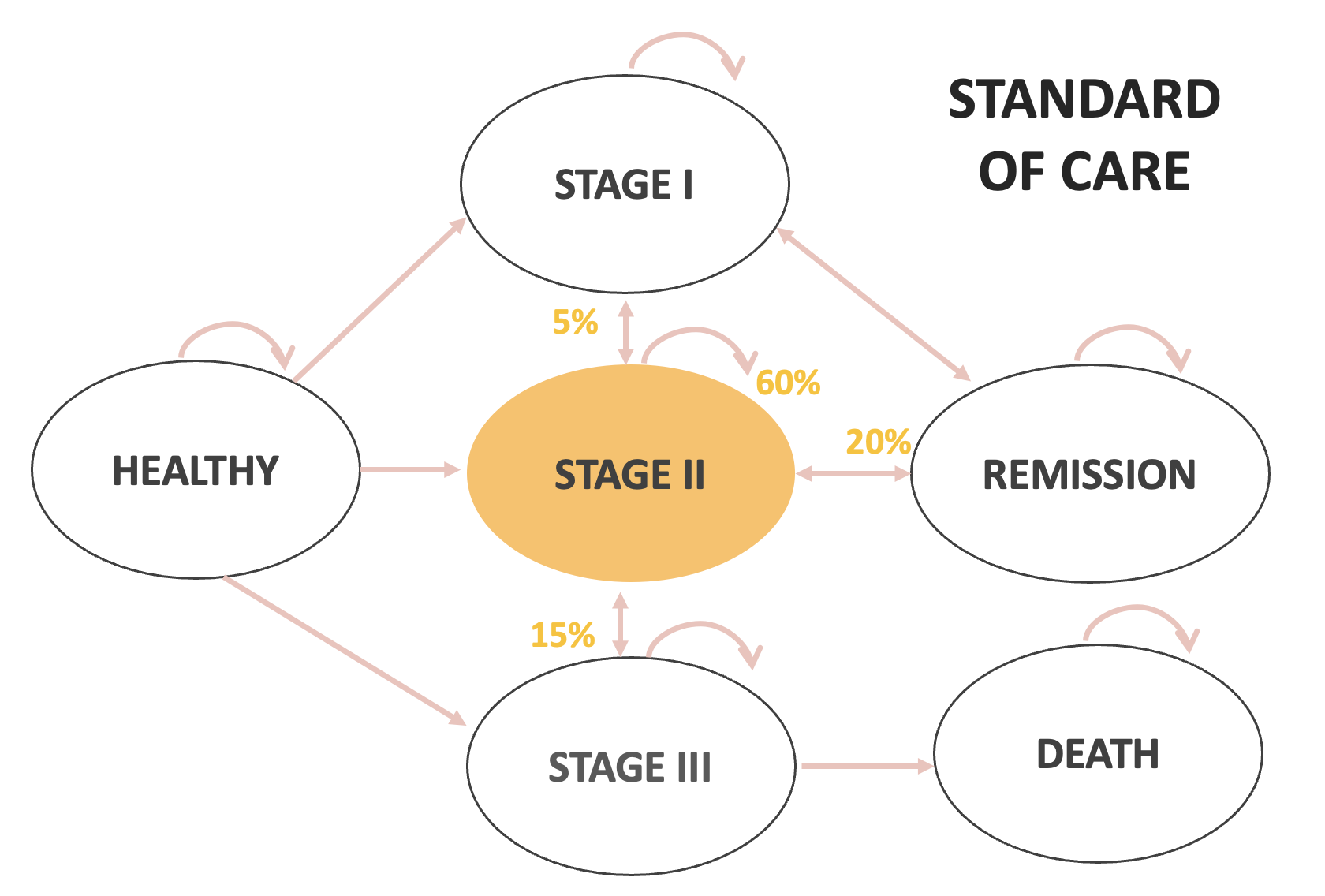
Ejemplo práctico

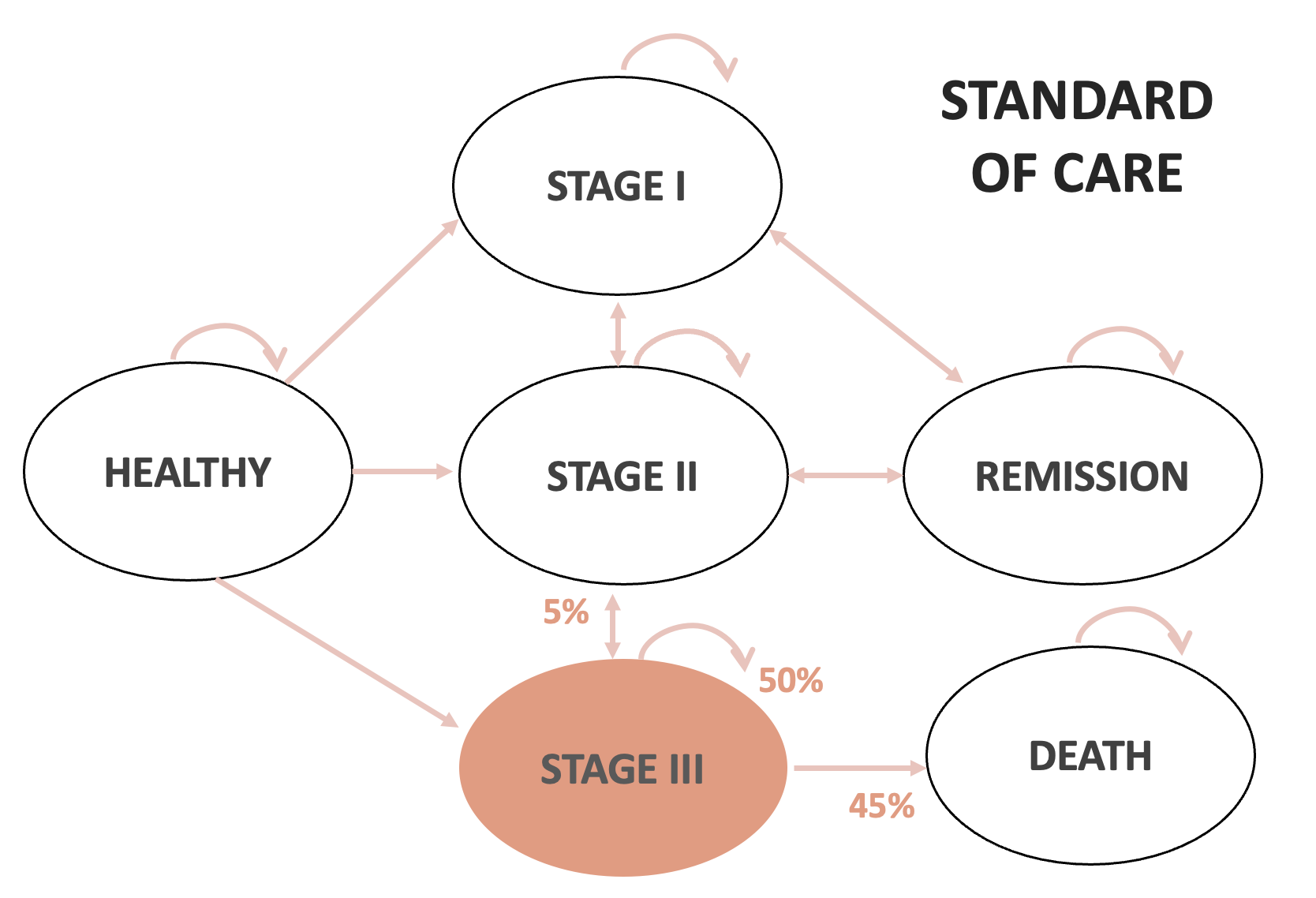
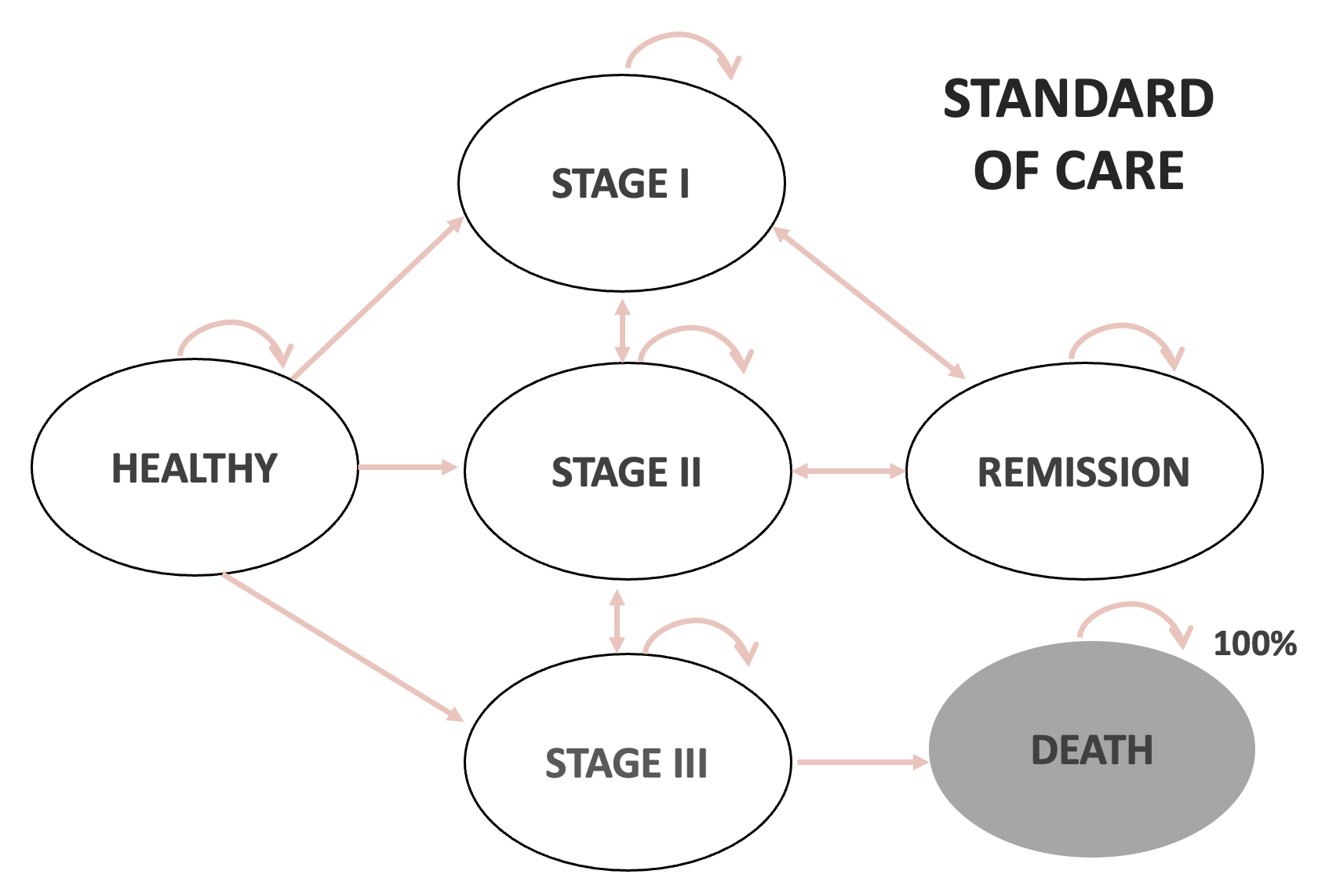
Ejemplo práctico

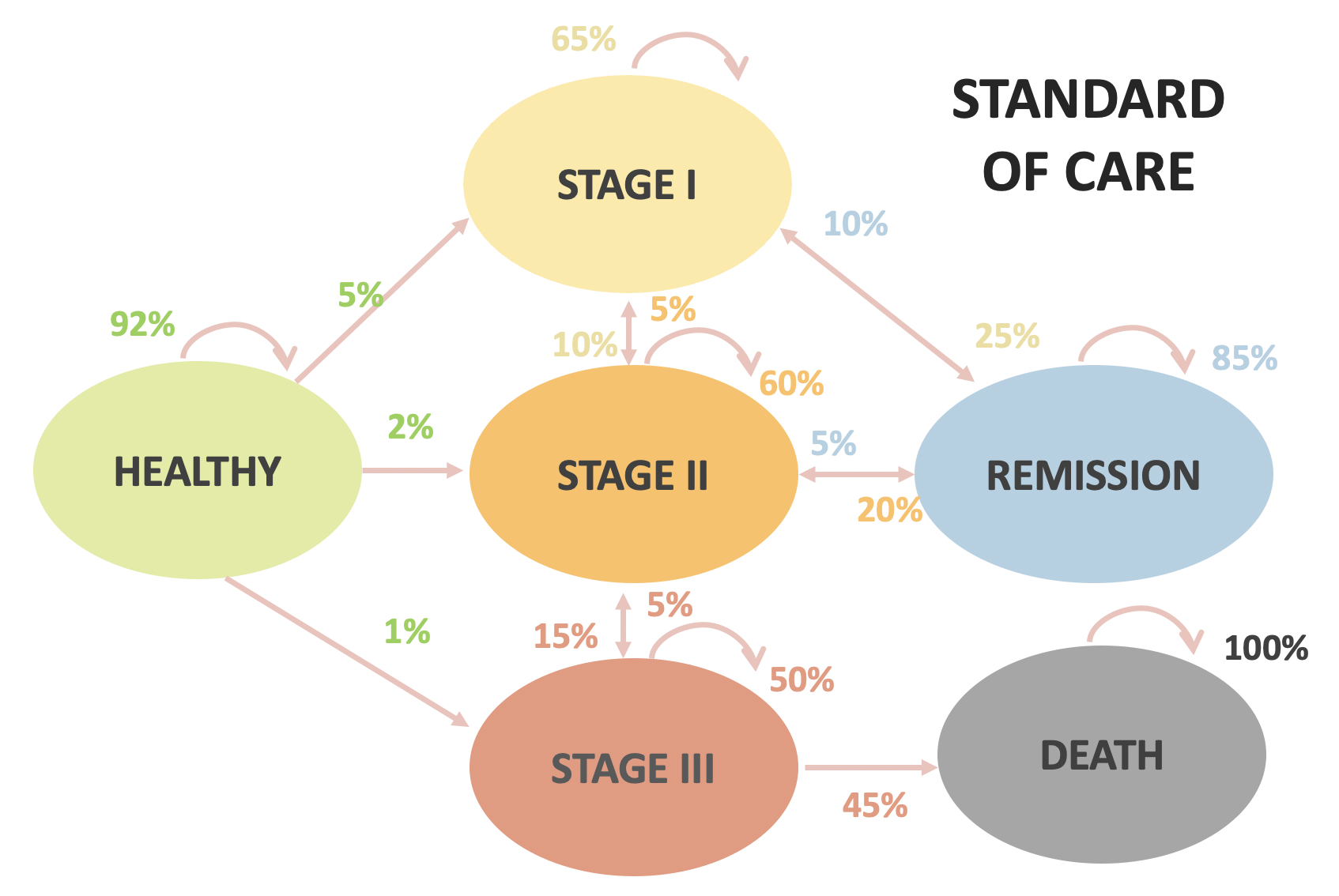
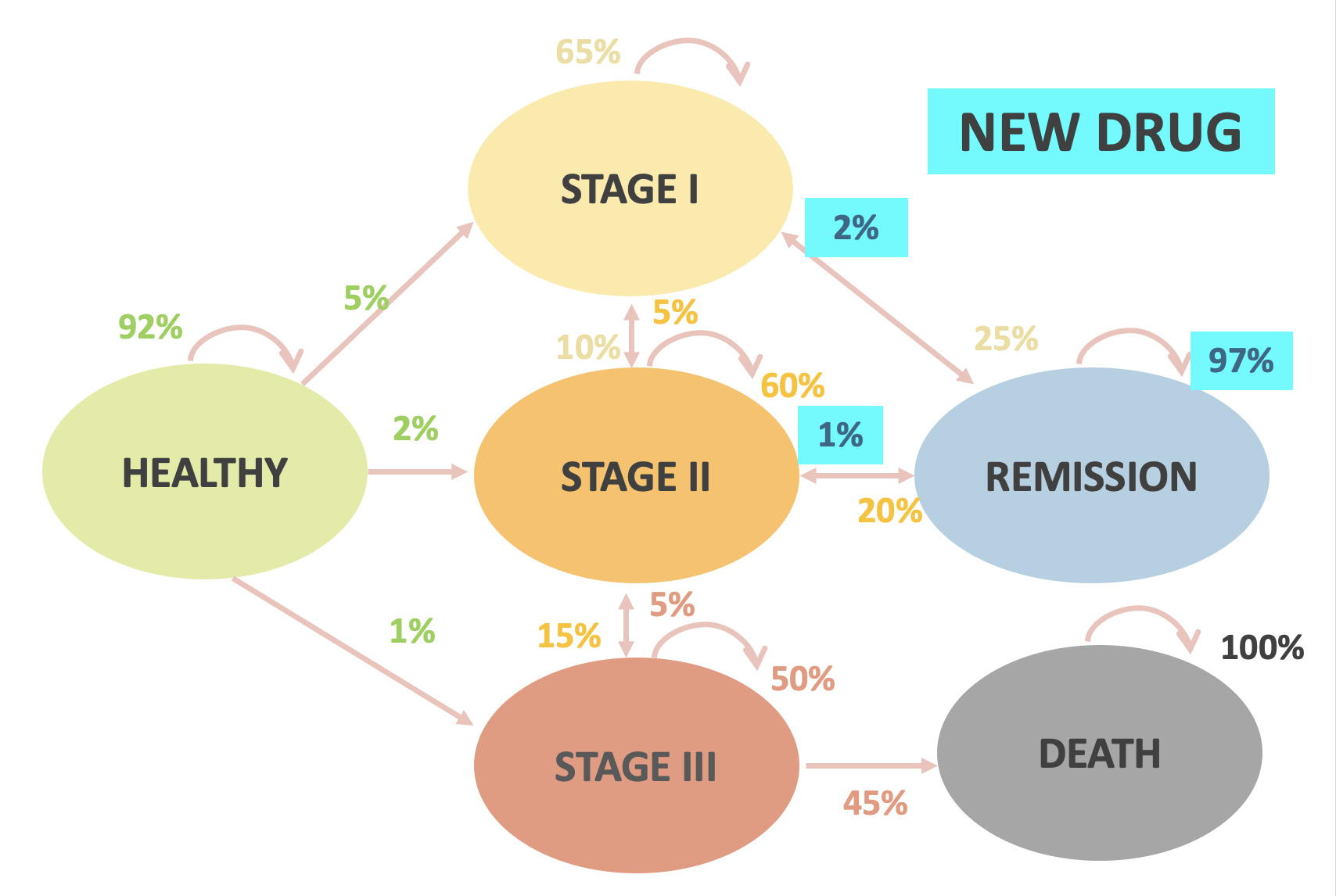
Ejemplo práctico

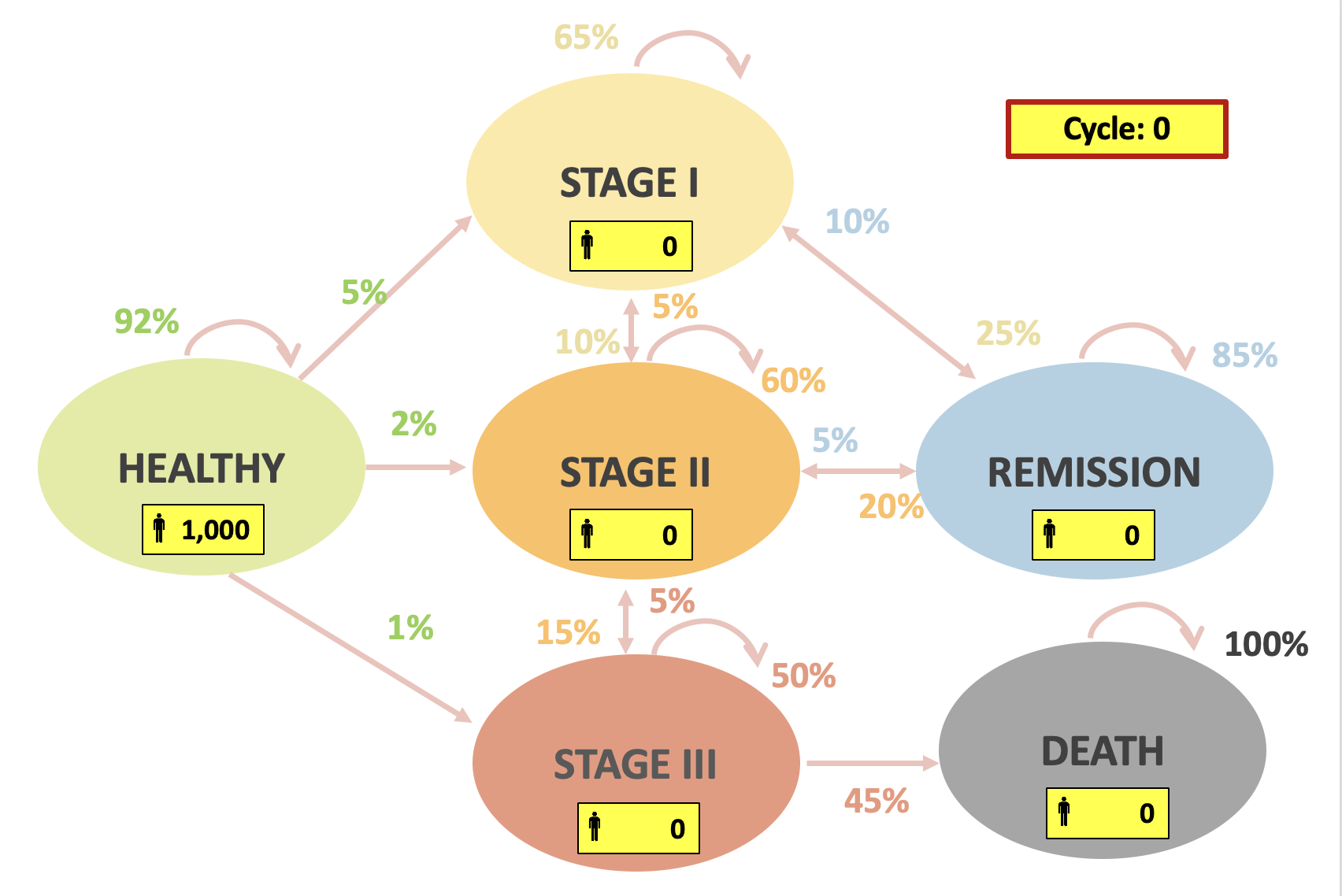
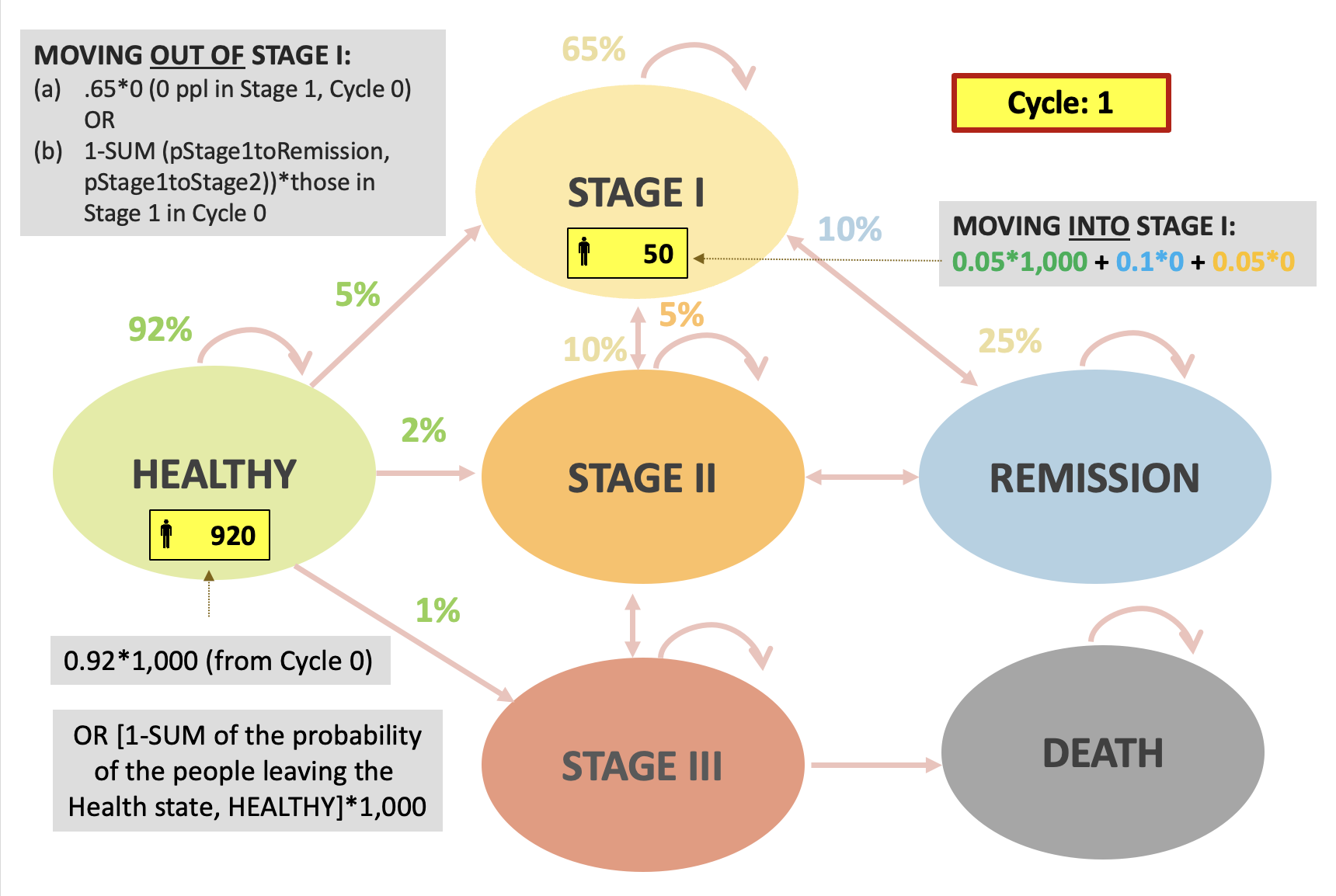
Ejemplo práctico

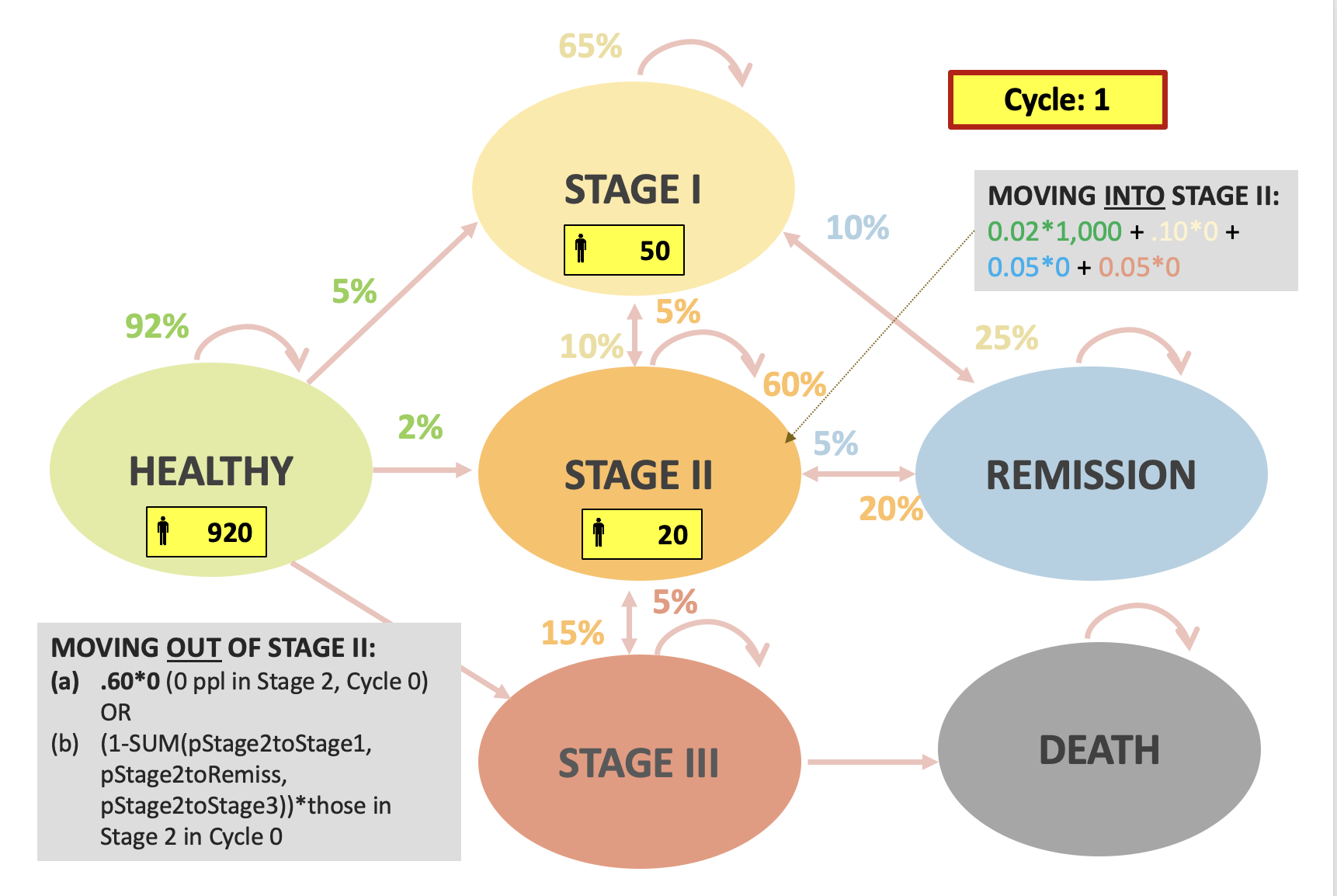
Cálculo de resultados

Un ejemplo de Rastreo de Markov (horizonte de 75 años)

Ciclo Sano Enfermo Muerto
0 1.000 0.000 0.000
1 0.856 0.138 0.007
2 0.732 0.253 0.015
3 0.626 0.349 0.025
4 0.536 0.429 0.035
5 0.458 0.495 0.046
… … … …
75 (End) 0 0.282 0.718

Rastreos de Markov

  • A menudo modelamos varias estrategias que compiten entre sí.
  • Cada estrategia tiene su propia matriz de probabilidad de transición.
  • Por lo tanto, cada estrategia tendrá su propio rastreo de Markov.

Cálculo de resultados

  • Con nuestros rastreos de Markov completos, podemos calcular los resultados esperados (por ejemplo, costos, AVAC, AVAD, etc.).
  • Al igual que hicimos con los árboles de decisión, tenemos que definir los “pagos” para cada estado de salud.

Definición de los resultados

  • Costo de los resultados: Costo de estar sano, enfermo, muerto (incluido cualquier costos adicionales del tratamiento/intervención, si procede).
  • Resultados AVAC: Peso de la utilidad de estar sano (normalmente 1,0), enfermo muerto (normalmente 0,0).
  • Resultados AVAD: Pesos de discapacidad de estar enfermo (AVD) y esperanza de vida restante basada en la tabla de vida de referencia (AVP)

Definición de las compensaciones

  • Podemos calcular la retribución total de cada ciclo multiplicando el número o la fracción de la cohorte en cada estado de salud por su valor de compensación y sumándolos.

Ejemplo de rastreo de Markov (dos ciclos):

Ciclo Sano Enfermo Muerto
0 1.000 0.000 0.000
1 0.856 0.138 0.007

Ejemplo: Años de vida

  • Construiremos nuestro ejemplo utilizando un resultado simple: años de vida esperados bajo una estrategia dada.
  • Resultados:
    • Sano: 1,0
    • Enfermo: 1,0 [Siguen vivos!]
    • Muerto: 0.0

Ejemplo: Años de vida

  • Para obtener la “retribución” total de un ciclo determinado, multiplicamos la fracción de la cohorte en un estado de salud dado por la retribución asociado a ese estado de salud.
  • Haga esto para cada estado de salud y súmelos para obtener el total.
Ciclo Sano Enfermo Muerto AV
0 1.000 0.000 0.000
1 0.856 0.138 0.007

Ejemplo: Años de vida

Cuál es la retribución en AV para el ciclo 0?

Ciclo Sano Enfermo Muerto AV
0 1.000 0.000 0.000
1 0.856 0.138 0.007

Ejemplo: Años de vida

Cuál es la retribución en AV para el ciclo 0?

Ciclo Sano Enfermo Muerdo AV
0 1.000 0.000 0.000 1.0 = 1.0 * 1.0 + 0.0 * 1.0 + 0.0 * 0.0
1 0.856 0.138 0.007

Ejemplo: Años de vida

Cuál es la retribución en AV para el ciclo 1?

Ciclo Sano Enfermo Muerte AV
0 1.000 0.000 0.000 1.0
1 0.856 0.138 0.007 0.994 = 0.856 * 1.0 + 0.138 * 1.0 + 0.007 * 0.0

… y así sucesivamente.

Ejemplo: Años de vida

Ciclo Sano Enfermo Muerto AV
0 1.000 0.000 0.000 1
1 0.856 0.138 0.007 0.993
2 0.732 0.253 0.015 0.985
3 0.626 0.349 0.025 0.975
4 0.536 0.429 0.035 0.965
5 0.458 0.495 0.046 0.954
… … … …
75 (End) 0 0.282 0.718 0.282

Ejemplo: Costos

  • Ahora supongamos que queremos calcular los costos
  • Retribuciones:
    • Sano: $0
    • Enfermo: $1,000
    • Muerto: $0

Ejemplo: Costos

¿Cuál es el costo del ciclo 0?

Ciclo Sano Enfermo Muerto Costo
0 1.000 0.000 0.000
1 0.856 0.138 0.007

Ejemplo: Costos

¿Cuál es el costo del ciclo 0?

Ciclo Sano Enfermo Muerto Costo
0 1.000 0.000 0.000 0 = 1.00 * 0 + 0.0 * 1000 + 0.0 * 0
1 0.856 0.138 0.007

Ejemplo: Costos

¿Cuál es el costo del ciclo 1?

Ciclo Sano Enfermo Muerto Costo
0 1.000 0.000 0.000 0
1 0.856 0.138 0.007 138 = 0.856*0+0.138*1000+0.007*0

… y así sucesivamente.

Otros resultados

  • Podemos repetir un proceso similar para los resultados sanitarios (por ejemplo, AVAC, AVD) multiplicando el “resultado” (por ejemplo, el peso de la utilidad, el peso de la discapacidad) para un estado de salud determinado por la fracción de la cohorte que se encuentra en ese estado de salud en el ciclo.

Cálculo de los resultados totales esperados

Resultados totales

Total de años de vida

Veamos el rastreo de Markov y los resultados del ciclo para el resultado años de vida.

Ciclo Sano Enfermo Muerto AV (ciclo único)
0 1.000 0.000 0.000 1
1 0.856 0.138 0.007 0.993
2 0.732 0.253 0.015 0.985
3 0.626 0.349 0.025 0.975
4 0.536 0.429 0.035 0.965
5 0.458 0.495 0.046 0.954
… … … …
75 (End) 0 0.282 0.718 0.282

Años de vida

Podemos crear una nueva columna que acumule los años de vida en cada ciclo.

Ciclo Sano Enfermo Muerto AV (ciclo único) AV (cumulativo)
0 1.000 0.000 0.000 1 1
1 0.856 0.138 0.007 0.993 1 + 0.993 = 1.993
2 0.732 0.253 0.015 0.985
3 0.626 0.349 0.025 0.975
4 0.536 0.429 0.035 0.965
5 0.458 0.495 0.046 0.954
… … … … …
75 (End) 0 0.282 0.718 0.282

Años de vida

Ciclo Sano Enfermo Muerto AV (ciclo único) AV (cumulativo)
0 1.000 0.000 0.000 1 1
1 0.856 0.138 0.007 0.993 1.993
2 0.732 0.253 0.015 0.985 1 + 0.993 + 0.985 = 2.978
3 0.626 0.349 0.025 0.975
4 0.536 0.429 0.035 0.965
5 0.458 0.495 0.046 0.954
… … … … …
75 (End) 0 0.282 0.718 0.282

Años de vida

  • Los AV culmulativos para un individuo empezando en el estado sano es 44.825

  • Notamos que este resultado es dentro de un horizonte de 75 años.

Ciclo Sano Enfermo Muerto AV (ciclo único) AV (cumulativo) AV (ciclo único) AV (ciclo único) LY (cumulative)
0 1.000 0.000 0.000 1 1
1 0.856 0.138 0.007 0.993 1.993
2 0.732 0.253 0.015 0.985 2.978
3 0.626 0.349 0.025 0.975 3.954
4 0.536 0.429 0.035 0.965 4.919
5 0.458 0.495 0.046 0.954 5.872
… … … … … …
75 (End) 0 0.282 0.718 0.282 44.825

Resultados totales

  • Podemos hacer un ejercicio similar para obtener los costos totales, los AVAC totales, los AVAD totales, etc.
  • Sin embargo, no es tan sencillo. Hay algunas complicaciones adicionales.
    • Descuentos
    • Corrección cíclica

Corrección de ciclo

El problema

  • En la vida real, los eventos podrían ocurrir en cualquier punto de un ciclo dado, pero un modelo de Markov asume que todos los eventos ocurren al principio o al final de cada ciclo

  • El tiempo es continuo, también lo son las curvas de supervivencia

  • Cuando discretizamos el tiempo utilizando una longitud de ciclo fija, podemos hacer dos supuestos

    • Supongamos que se trata de un simple proceso sano -> muerto

El problema

Asumiendo que la muerte ocurre al final del ciclo (A)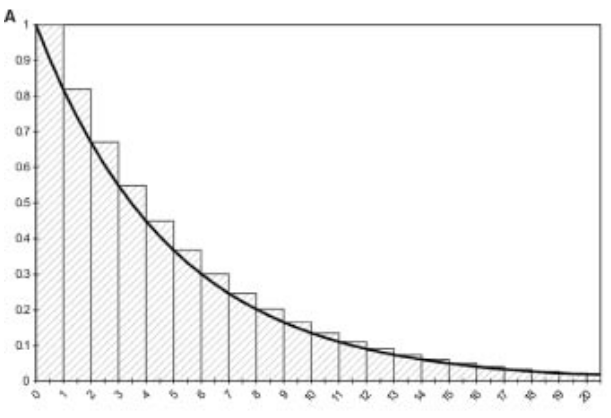

Sobreestima la pertenencia a un estado de salud

Asumiendo que la muerte ocurre al inicio del ciclo (B)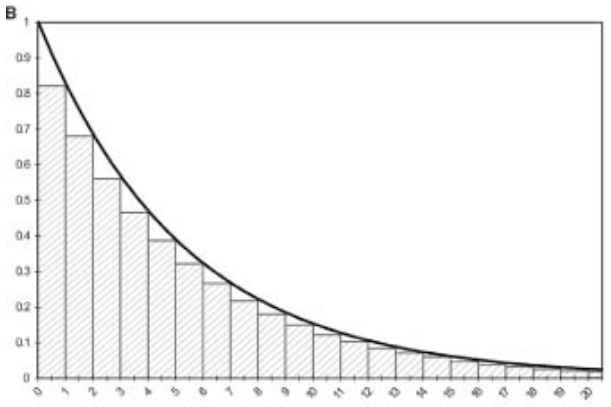

Subestima la pertenencia a un estado de salud

Source

El problema

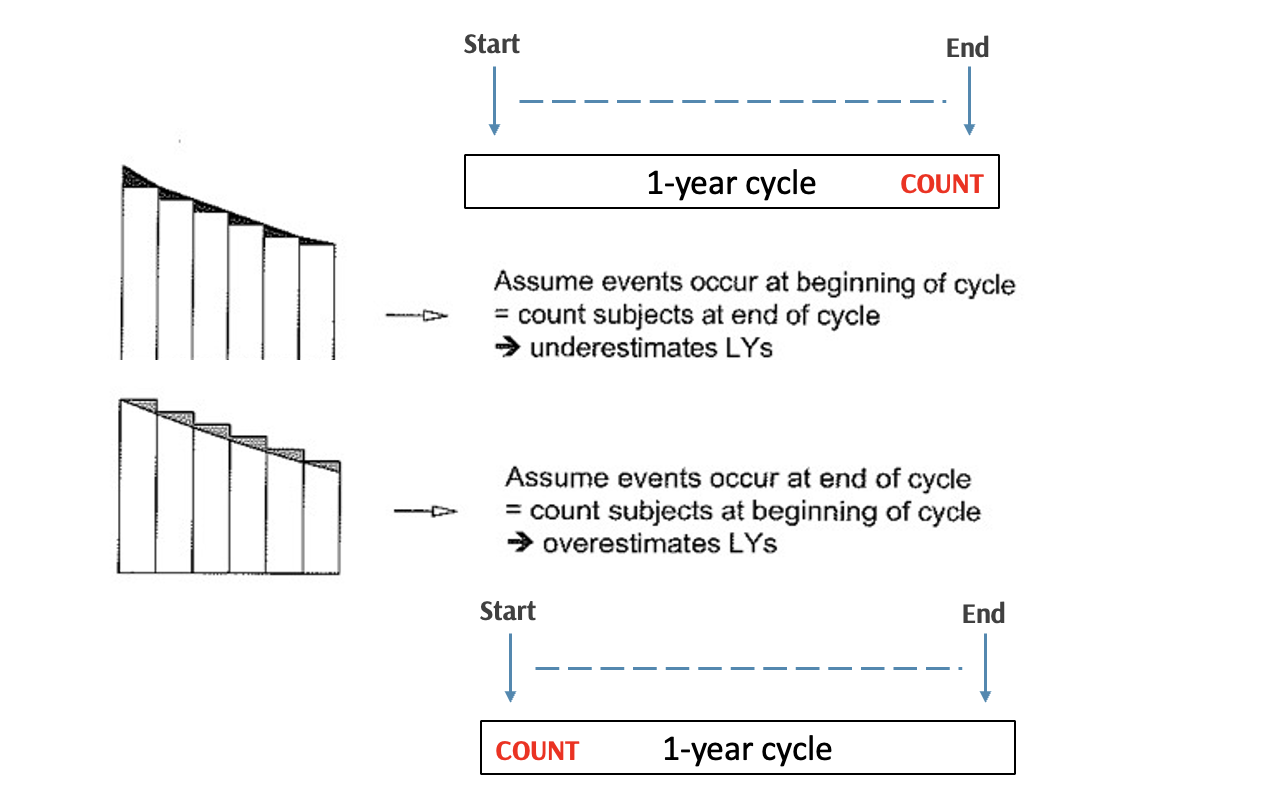
Corrección mitad del ciclo

Source

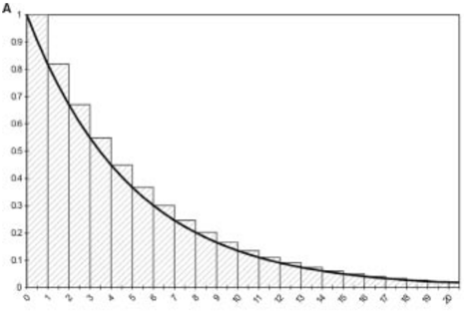
Corrección mitad del ciclo

Source

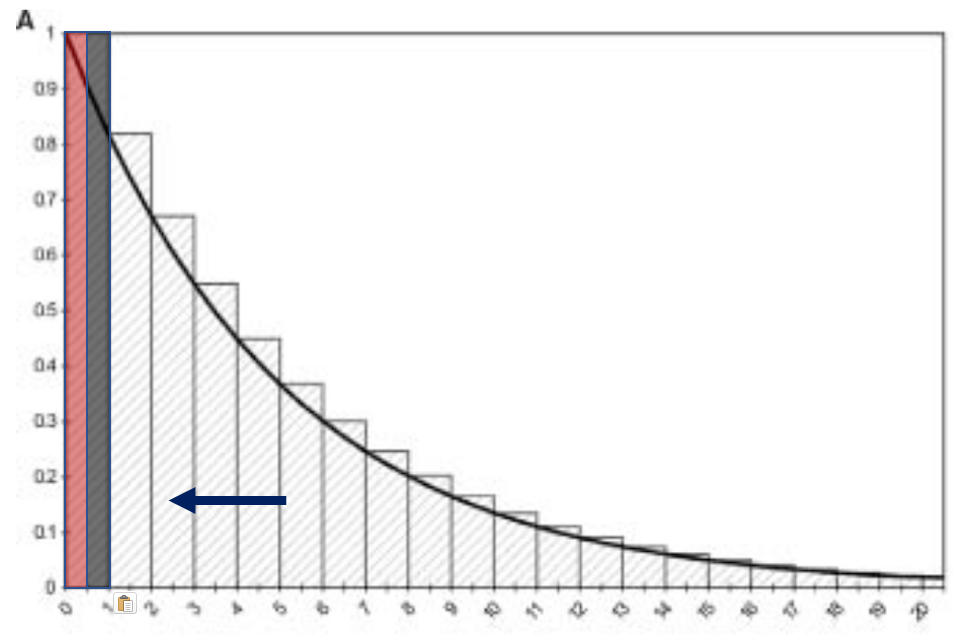
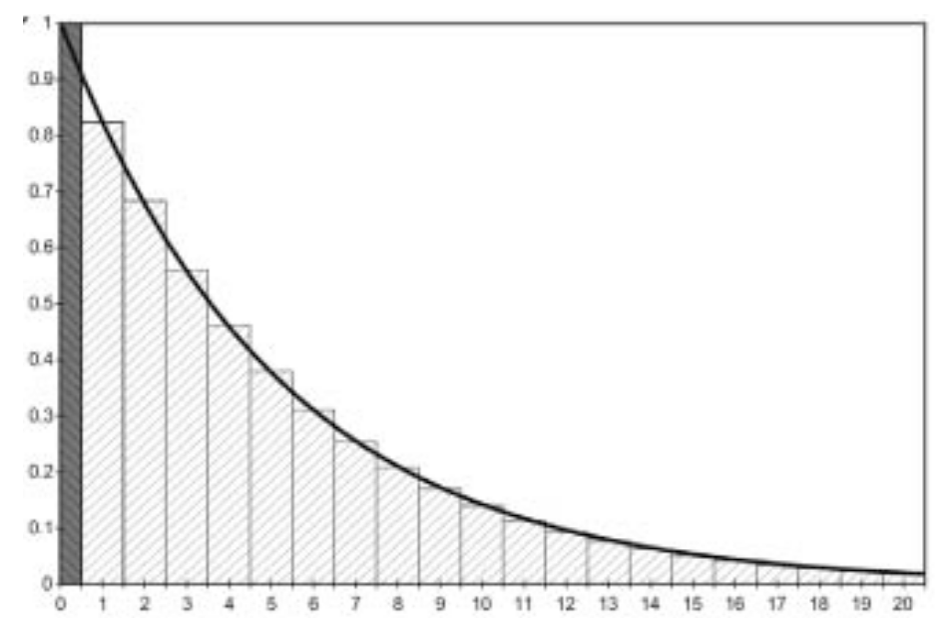
Corrección mitad del ciclo

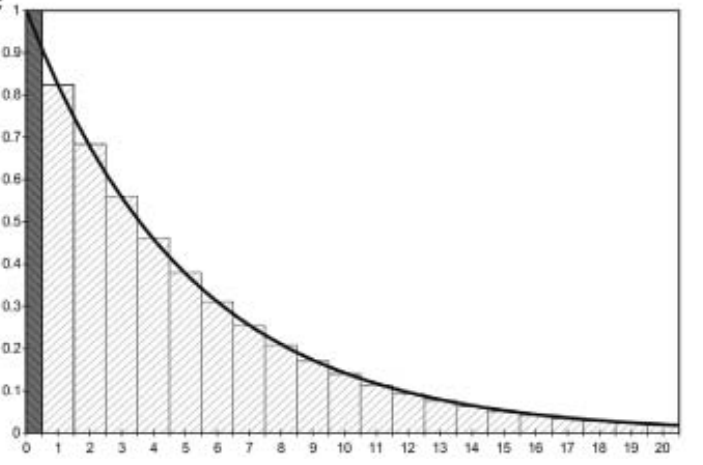
  • Multiplicar los resultados por 1/2 en el primer y último ciclo.

  • Desplazar la curva calculada de pertenencia a un estado discreto hacia la izquierda en 1/2 ciclo.

  • Esencialmente asumiendo que los eventos ocurren en la mitad del ciclo

Source

Corrección mitad del ciclo


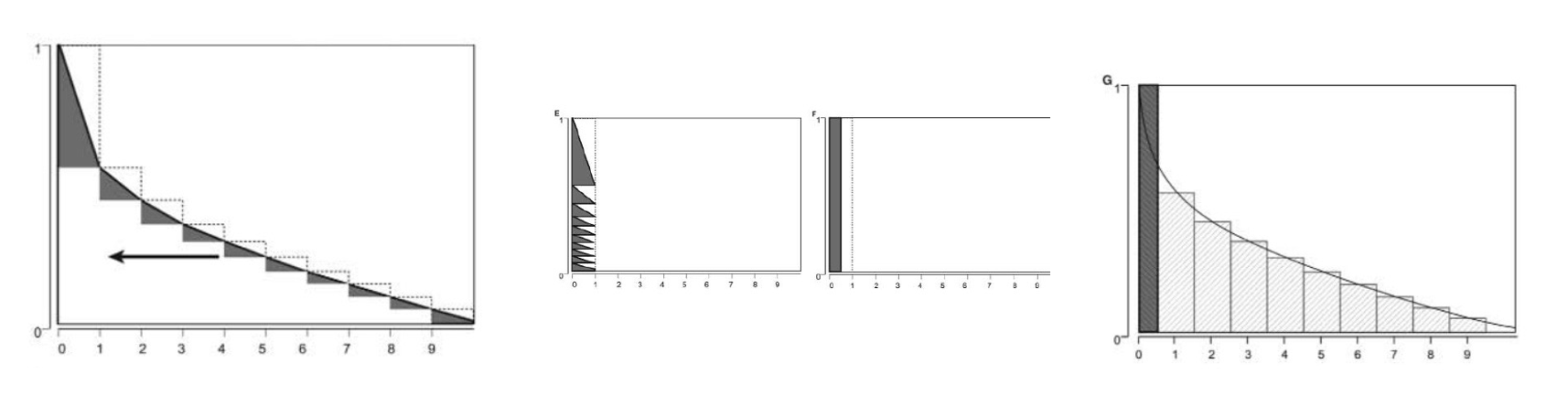
Aplicar corrección mitad del ciclo a nuestro rastreo de Markov…

Corrección mitad del ciclo

  • Multiplicar los resultados por 1/2 en el primer y último ciclo.
Ciclo Sano Enfermo Muerto LY (single Ciclo, adjusted) LY (cumulative)
0 1.000 0.000 0.000 1*0.5 0.5
1 0.856 0.138 0.007 0.993 0.5 + 0.993 = 1.493
2 0.732 0.253 0.015 0.985 2.478
3 0.626 0.349 0.025 0.975 3.454
4 0.536 0.429 0.035 0.965 4.419
5 0.458 0.495 0.046 0.954 5.372
… … … … … …
75 (End) 0 0.282 0.718 0.282 *0.5 44.184

Este número es menor que nuestra estimación original sin corrección de medio ciclo (¡44,825!)

Resumen

  • Una vez que tenemos los resultados totales (descontados, corregidos por medio ciclo) para cada estrategia, podemos pasar a realizar un análisis costo-efectividad incremental.

Markov Models

Pros Contras
Puede modelar sucesos repetidos Sólo puede transitar una vez por ciclo
Puede modelizar eventos clínicos más complejos y longitudinales Acortar el ciclo puede plantear retos informáticos.
No requiere muchos cálculos; es eficiente de modelar y depurar. Acortar el ciclo puede provocar una “explosión de estados” si se utilizan estados túnel

Volver al sitio web